Общий способ вычисления моментов инерции сложных сечений.

При проверке прочности частей конструкций нам приходится встречаться с сечениями довольно сложной формы, для которых нельзя вычислить момент инерции таким простым путем, каким мы пользовались для прямоугольника и круга.

Таким сечением может быть, например, тавр (Рис.5 а) кольцевое сечение трубы, работающей на изгиб (авиационные конструкции) (Рис.5, б), кольцевое сечение шейки вала или еще более сложные сечения. Все эти сечения можно разбить на простейшие, как-то: прямоугольники, треугольники, круги и т.д. Можно показать, что момент инерции такой сложной фигуры является суммой моментов инерции частей, на которые мы ее разбиваем.

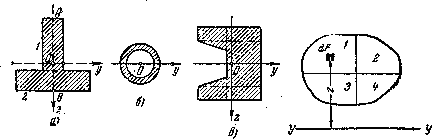
Рис.5. Сечения типа тавр — а) и кольцо б)

Известно, что момент инерции любой фигуры относительно оси у—у равен:

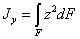
где z—расстояние элементарных площадок 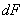до оси у—у.

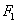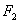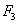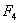Разобьем взятую площадь на четыре части: , , и . Теперь при вычислении момента инерции можно сгруппировать слагаемые в подинтегральной функции так, чтобы отдельно произвести суммирование для каждой из выделенных четырех площадей, а затем эти суммы сложить. Величина интеграла от этого не изменится.

Наш интеграл разобьется на четыре интеграла, каждый из которых будет охватывать одну из площаде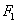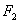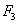й , , и :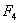

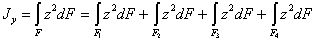
Каждый из этих интегралов представляет собой момент инерции соответствующей части площади относительно оси у — у; поэтому

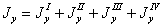
где 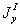— момент инерции относительно оси у — у площади 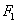, 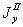— то же для площади 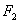и т. д.

Полученный результат можно формулировать так: момент инерции сложной фигуры равен сумме моментов инерции составных ее частей. Таким образом, нам необходимо уметь вычислять момент инерции любой фигуры относительно любой оси, лежащей в ее плоскости.

Решение этой задачи и составляет содержание настоящей и последующих двух собеседований.