Деформации при действии собственного веса.

При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придется учесть, что относительное удлинение различных участков стержня будет переменным, как и напряжение . Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной , находящегося на расстоянии 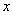от конца стержня (Рис.4).

Рис.4. Расчетная модель бруса с учетом собственного веса.

Абсолютное удлинение этого участка равно

Полное удлинение стержня 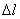равно:

Величина 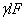представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:

подразумевая под S внешнюю силу и половину собственного веса стержня.

Что же касается деформаций стержней равного сопротивления, то, так как нормальные напряжения во всех сечениях одинаковы и равны допускаемым 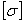, относительное удлинение по всей длине стержня одинаково и равно

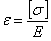
Абсолютное же удлинение при длине стержня l равно:

где обозначения соответствуют приведенным на рис.1.

Деформацию ступенчатых стержней следует определять по частям, выполняя подсчеты по отдельным призматическим участкам. При определении деформации каждого участка учитывается не только его собственный вес, но и вес тех участков, которые влияют на его деформацию, добавляясь к внешней силе. Полная деформация получится суммированием деформаций отдельных участков.