Закон сохранения энергии в механике

Полная механическая энергия Е тела равна сумме кинетической Е_к и потенциальной Е_n энергий.

Е = Е_к + Е_n (4.20)

Чтобы вывести закон сохранения механической энергии рассмотрим замкнутую систему, т.е. систему, где действуют только консервативные силы, а действия внешних сил отсутствуют.

Допустим, что система состоит из материальных точек m₁, m₂, …, m_n, движущихся со скоростями u₁, u₂, …, u_n .

Если на каждую точку действуют только внутренние консервативные силы 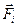, то по II закону Ньютона получим:

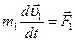
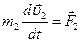
………… (4.21)

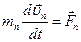
Пусть все точки за время dt совершают перемещения
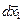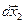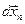, ,…, . Умножим каждое из уравнений (4.21) на соответствующие перемещения с учетом, что .

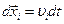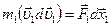
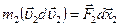
………… (4.22)

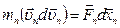
После сложения этих уравнений получим

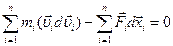(4.23)

Первый член уравнения (4.23) представляет собой приращение кинетической энергии dE_k

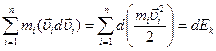(4.24)

Второй член уравнения (4.23) есть работа, совершаемая внутренними консервативными силами за счет убыли потенциальной энергии dE_n

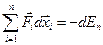(4.25)

Подставив (4.24) и (4.25) в уравнение (4.23) получим

dE_k + dE_n = 0 (4.26)

откуда полная механическая энергия Е тела будет равна

Е = Е_к + Е_п = const (4.27)

Выражение (4.27) представляет собой закон сохранения механической энергии: в замкнутой системе полная механическая энергия есть величина постоянная.

К началу

К следующей лекции К содержанию

К титулу