Энергия. Кинетическая и потенциальная энергии
Работа переменной силы. Мощность.
Если под действием силы F происходит движение и тело перемещается на величину S, то говорят, что сила совершает работу. Работа – скалярная физическая величина, равная произведению проекции силы Fs на направление перемещения на перемещение S.
А = Fs · S (4.1)
Эта формула справедлива для прямолинейного движения при Fs= const, а также когда угол между вектором силы 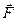 и перемещением
и перемещением 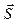 не изменяется. Учитывая, что Fs = F·cos
не изменяется. Учитывая, что Fs = F·cos 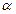 выражению (4.1) можно придать вид:
выражению (4.1) можно придать вид:
А = F · S cos 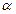 (4.2)
(4.2)
Другими словами, работу можно представить как скалярное произведение векторов 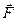 и
и 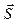 .
.
А = 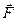 ·
· 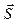 (4.3)
(4.3)
Из формулы (4.2) видно, что работа может иметь как положительное, так и отрицательное значение. Когда cos 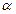 >0 (a – острый угол), работа положительна (А>0), при cos
>0 (a – острый угол), работа положительна (А>0), при cos 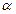 <0 (a – тупой угол), работа отрицательна (А<0).
<0 (a – тупой угол), работа отрицательна (А<0).
Единица работы – джоуль (Дж): 1 Дж = 1 Н·м.
 Работу можно изобразить графически. При Fs= const график силы представлен на рис. 4.1.
Работу можно изобразить графически. При Fs= const график силы представлен на рис. 4.1.
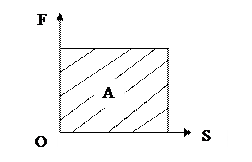
Рис. 4.1.
На графике видно, что работа равна площади заштрихованного прямоугольника.
Если работа совершается под действием переменной силы, т.е. F ≠ const (F = F (S)), то графически работа будет равна площади под кривой (рис. 4.2).
Чтобы найти работу переменной силы разобьем пройденный путь на элементарные отрезки пути dSi. Тогда работа на элементарном отрезке пути будет:
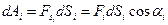 (4.4)
(4.4)
Если при прямолинейном движении элементарный отрезок пути выбрать таким, чтобы F = const и 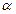 = const, то на пути от S1 до S2 работа будет равна:
= const, то на пути от S1 до S2 работа будет равна:
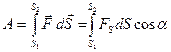 (4.5)
(4.5)
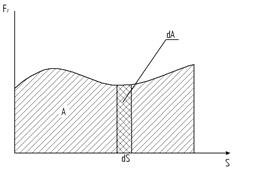
Рис. 4.2
Для характеристики быстроты совершения работы вводится понятие мощности. Мощность N – физическая величина, равная отношению работы ΔА к промежутку времени Δt, в течение которого она совершается
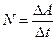 (4.6)
(4.6)
Если тело движется со скоростью u под действием силы F, то мощность равна произведению проекции силы на перемещение на скорость тела
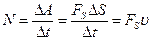 (4.7)
(4.7)
Если мощность со временем изменяется, то вводится понятие мгновенной мощности
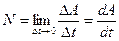 (4.8)
(4.8)
Мощность измеряется в ваттах: 1Вт = 1Дж/с.
Энергия. Кинетическая и потенциальная энергии
Тот факт, что тела могут совершать работу над другими телами, означает, что данные тела обладают энергией. Физическая величина, характеризующая способность тела или системы тел совершать работу называется энергией. Или иначе: работа – представляет собой количественную характеристику процесса обмена энергией между взаимодействующими телами. Энергия является универсальной мерой движения и взаимодействия всех видов материи.
В зависимости от вида движения различаются формы энергии: механическая, тепловая, электромагнитная, ядерная и др. Энергия может переходить из одной формы в другую.
В механике различают два вида энергии: кинетическую и потенциальную.
Кинетическая энергия определяется работой, которая необходима, чтобы вызвать движение. Кинетическая энергия – эта энергия движения, любое движущееся тело обладает кинетической энергией
dА= F×dS (4.9)
где, 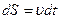 , F =
, F = 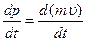
Если скорость изменяется от u1 до u2, то
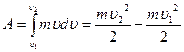 (4.10)
(4.10)
Работа совершается за счет убыли кинетической энергии
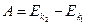 (4.11)
(4.11)
Из (4.10) и (4.11) видно, что кинетическая энергия равна
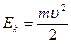 (4.12)
(4.12)
Потенциальной энергией называется та часть механической энергии, которая определяется взаимодействием тел (частей тела) и зависит от их взаимного расположения. Если взаимодействие осуществляется через силовое поле и работа не зависит от траектории движения, то такие поля называются потенциальными. Силы, действующие в потенциальных полях, называются консервативными. Силы являются неконсервативными (диссипативными), если работа, совершаемая ими, зависит от траектории. Пример неконсервативных сил – силы трения.
Каждой точке потенциального поля соответствует сила F, действующая на тело и потенциальная энергия En. Установим связь между ними.
В потенциальном поле работа совершается за счёт убыли потенциальной энергии.
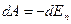 (4.13)
(4.13)
C другой стороны, работа есть скалярное произведение силы F на перемещение dr, т.е.
dA = 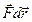 = Fsdr (4.14)
= Fsdr (4.14)
из соотношений (4.13) и (4.14) получим
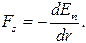 (4.15)
(4.15)
Для проекций силы 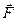 на оси х, у, z получим
на оси х, у, z получим
Fx = – 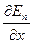 Fy= –
Fy= – 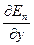 Fz = –
Fz = – 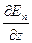 (4.16)
(4.16)
В векторном виде
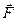 = – qrad En, (4.17)
= – qrad En, (4.17)
т.е. вектор силы равен градиенту потенциала с обратным знаком.
Из математики известно, что
grad En= 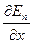
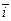 +
+ 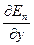
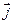 +
+ 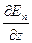
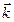 (4.18)
(4.18)
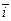 ,
, 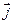 ,
, 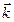 – единичные векторы координатных осей
– единичные векторы координатных осей
Градиент обозначается не только через «grad», но и символом 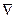 .
.
Выражение (4.17) можно переписать в виде
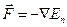 (4.19)
(4.19)
где, 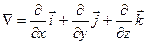 – оператор Гамильтона или набла-оператором.
– оператор Гамильтона или набла-оператором.
Дата добавления: 2015-10-26; просмотров: 704;
