Решение. 1.Касательное ускорение определяется как at = dV/dt

1.Касательное ускорение определяется как a_t = dV/dt

Уравнение скорости: v = dS/dt

Скорость будет равна v = 2 * 2,5t + 1,2; v = 5t + 1,2 (м/с).

Касательное ускорение: а_t = v' = 5 м/с².

Вывод: касательное ускорение не зависит от времени, оно посто­янно.

2. Нормальное ускорение: а_п = v²/r

Скорость на второй секунде будет равна v₂ = 5*2 + 1,2 = 11,2 м/с.

Величина нормального ускорения: а_п2 = (11,2)²/10 = 12,54 м/с² .

3. Полное ускорение:

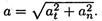
Полное ускорение в конце второй секунды:

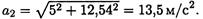
4. Нормальное ускорение направлено перпендикулярно скорости к центру дуги.

Касательное ускорение направлено по касательной к кривой и совпадает с направлением скорости, т. к. касательное ускорение — положительная величина (скорость растет).

Пример 3. По дуге, равной ¹/₄ длины окружности радиуса г = 16м (рис. 1.110), из положения А₀ в положение A₁ движется точка согласно уравнению s = πt². Определить скорость точки в момент, когда она проходит середину длины дуги A₀A₁, и в момент достижения положения A₁.