Расчет на поперечный изгиб

Для того чтобы понять характер работы элементов на податливых связях на поперечный изгиб, возьмем три балки, у которых нагрузки, пролеты и поперечные сечения одинаковые. Первая балка имеет цельное сечение (Ц), вторая – из двух брусьев без всяких связей (О) и третья – из двух брусьев с податливыми связями (П).

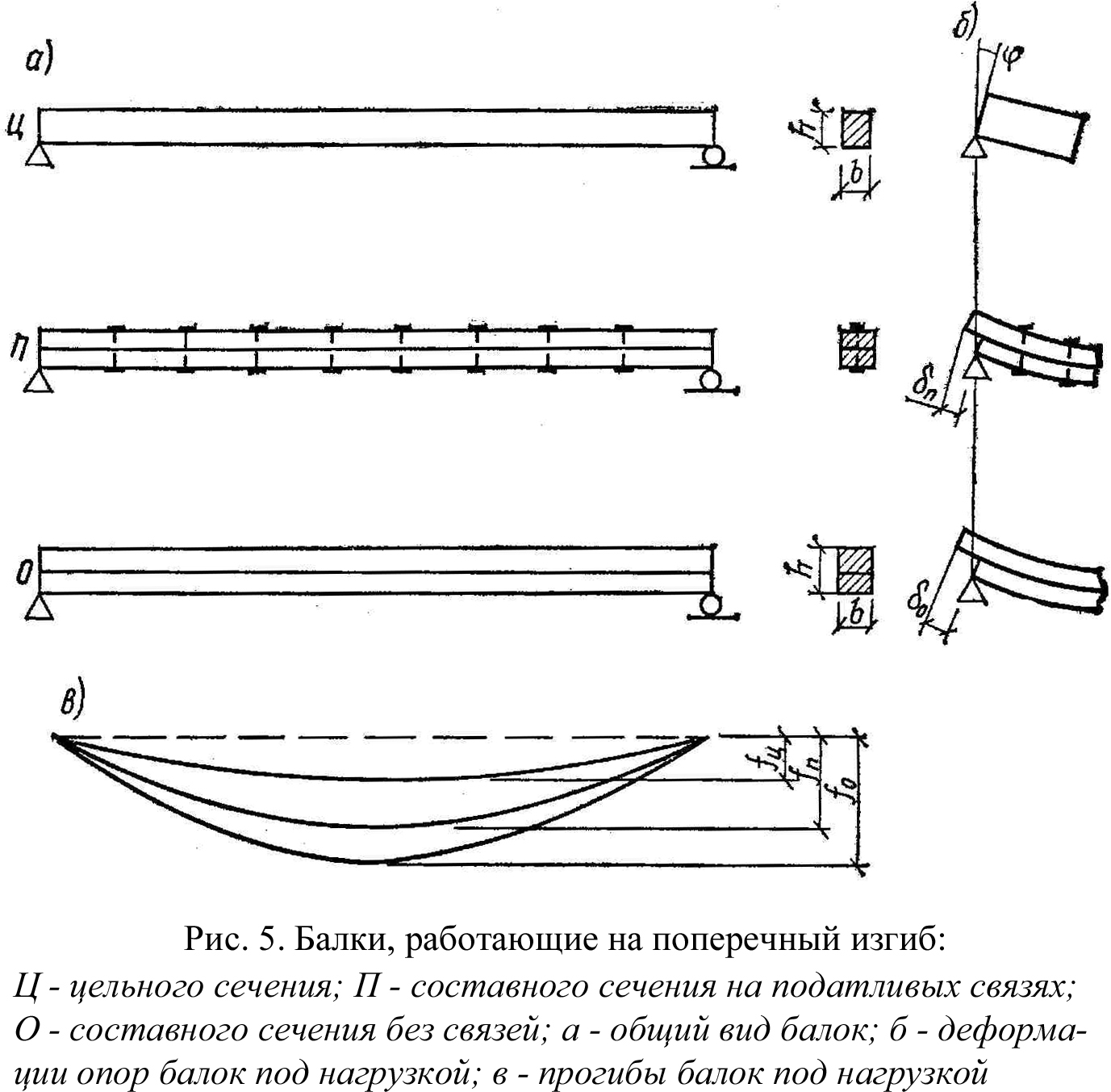Рисунок 5.5 – Балки, работающие на изгиб: Ц – цельного сечения; П – составного сечения на податливых связях; О – составного сечения без связей; а – общий вид балок; б – деформации балок под нагрузкой; в – прогибы балок под нагрузкой

При изгибе деформации составной балки на податливых связях будут больше деформаций балки цельного сечения, но меньше деформаций балки без связей: f_Ц<f_П<f_O.

При деформировании балки из двух брусьев без связей и с податливыми связями, на опорах произойдет смещение верхнего бруса относительно нижнего. У балки на податливых связях это смещение будет меньше, поскольку ему будут препятствовать болты. Следовательно, составная балка на податливых связях занимает промежуточное положение между балкой цельного сечения и составной балкой без связей. Поэтому можно записать:

W_Ц>W_П>W_О;

I_Ц>I_П>I_О;

f_Ц< f_П <f_О.

Из этих неравенств следует, что геометрические характеристики составной балки на податливых связях (I_Ц, W_Ц) можно выразить через геометрические характеристики балки цельного сечения, умноженные на коэффициенты k_w и k_ж, меньше 1, которые учитывают податливость связей, тогда:

, ;

, .

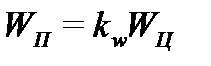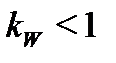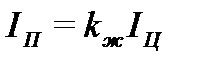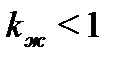Прогиб балки на податливых связях увеличивается соответственно уменьшению момента инерции:

.

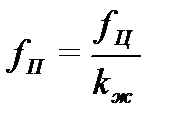Значения коэффициентов k_w и k_ж приведены в таблице 13 СНиП II-25-80 в зависимости от величины пролета и количества слоев в элементе. Расчет составной балки на податливых связях сводится, таким образом, к расчету балки цельного сечения с введением коэффициентов, учитывающих податливость связей:

1) нормальные напряжения определяются по формуле

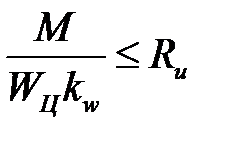, где

W_ц – момент сопротивления составной балки, как цельной;

k_w<1 – коэффициент, учитывающий податливость связей.

Аналогичным образом выполняется учет податливости связей и при расчете на устойчивость плоской формы изгиба.

2) прогиб составной балки на податливых связях в общем случае определяется по формуле

,

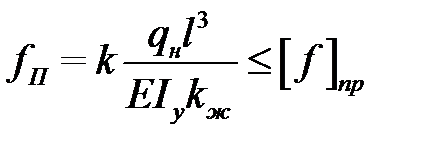где

I_y – момент сопротивления балки как цельной;

k_ж<1 – коэффициент, учитывающий сдвиг, вызванный податливостью связей.