Сжато-изгибаемые элементы

Сжато-изгибаемыми называются элементы, на которые одновременно действует изгибающий момент и центрально приложенное продольное сжимающее усилие. Так работают, например, верхние сжатые пояса ферм, нагруженные дополнительно межузловой поперечной нагрузкой.

В сечениях сжато-изгибаемого элемента возникают равномерные напряжения сжатия от продольных сил N и напряжения сжатия и растяжения от изгибающего момента М, которые суммируются.

Искривление сжато-изгибаемого элемента поперечной нагрузкой приводит к появлению дополнительного изгибающего момента с максимальным значением М_N=N·f,

где f – прогиб элемента с учетом дополнительного момента от продольной силы.

Расчет на прочность сжато-изгибаемых и внецентренно-сжатых элементов выполняют по формуле

,

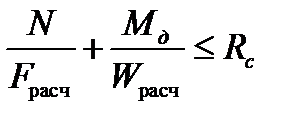где М_д – изгибающий момент от действия поперечных и продольных нагрузок, определяемый из расчета по деформированной схеме.

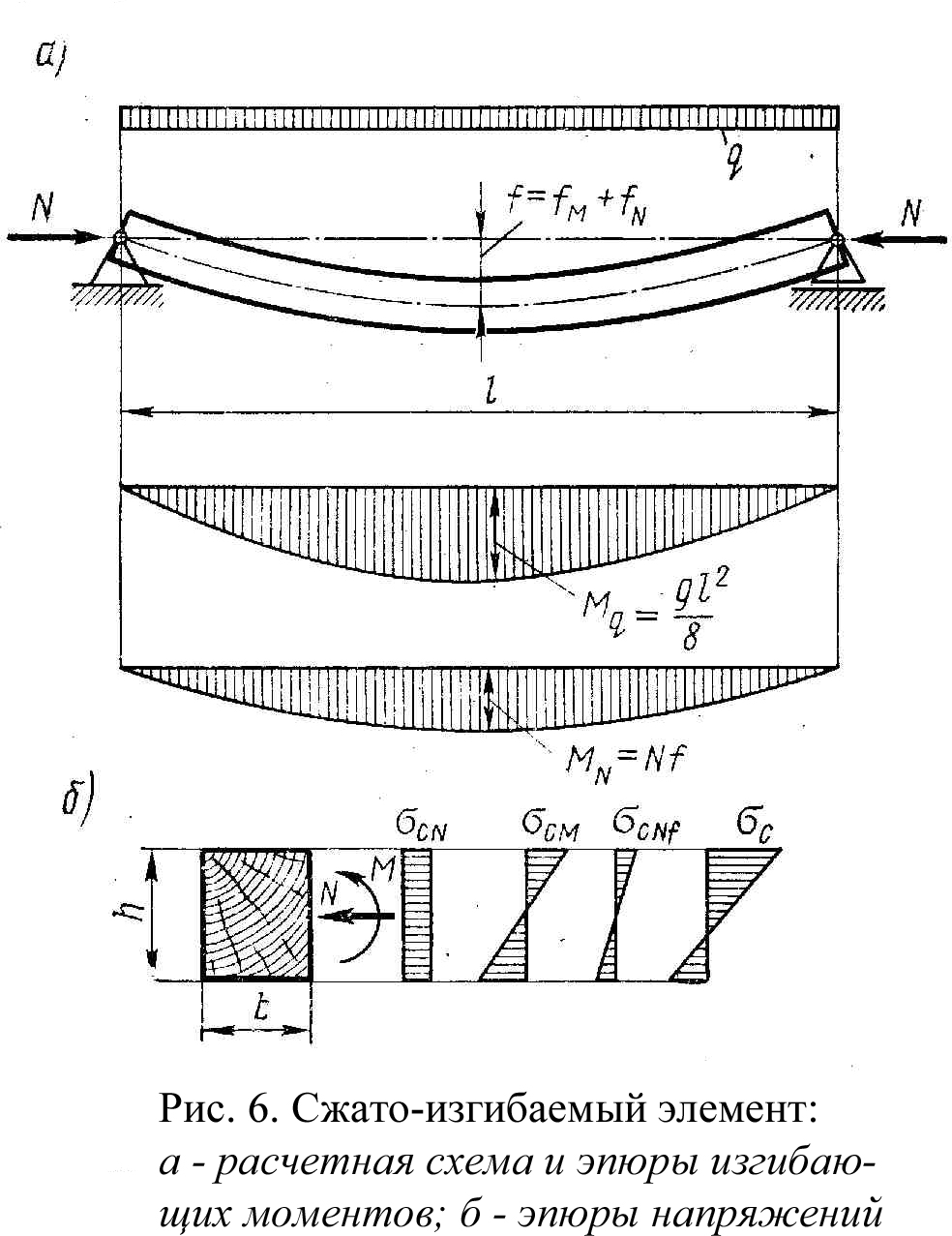Рисунок 2.6 – Сжато-изгибаемый элемент: а – расчетная схема и эпюры изгибающих моментов; б – эпюры напряжений

Для шарнирно-опертых элементов при симметричных эпюрах изгибающих моментов синусоидального, параболического и близких к ним очертаний

,

где

М – изгибающий момент в расчетном сечении без учета дополнительного момента от продольной силы;

ξ – коэффициент, изменяющийся от 0 до 1, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, определяемый по формуле:

,

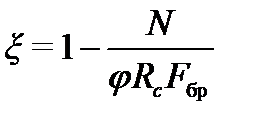где

φ – коэффициент продольного изгиба, определяемый по формуле (8) п.4.3 СНиП II-25-80

,

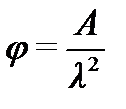где А=3000 – для древесины; А=2500 – для фанеры.

Кроме проверки на прочность, сжато-изгибаемые элементы проверяются на устойчивость по формуле:

,

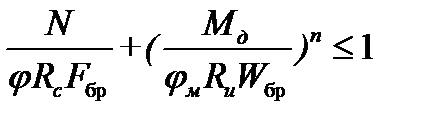Где F_бр – площадь брутто с максимальными размерами сечения элемента на участке l_p;

W_бр – максимальный момент сопротивления на участке l_p;

n=2 – для элементов без закрепления растянутой зоны из плоскости деформирования;

n=1 – для элементов, имеющих закрепления в растянутой зоне из плоскости деформирования;

φ – коэффициент продольного изгиба, определяемый по формуле, указанной выше для гибкости участка элемента расчетной длиной l_p из плоскости деформирования;

φ_м – коэффициент, формула для определения этого коэффициента была приведена ранее.