Решение. Освобождаем раму от связей и заменяем их действие реакциями NА, VA, VB (рис

Освобождаем раму от связей и заменяем их действие реакциями N_А, V_A, V_B (рис. 1.20, б). Получили плоскую систему произвольно расположенных сил.

Выбираем систему координат (см. рис. 1.20, б) и составляем уравнения равновесия:

где Р₂ cos α — вертикальная составляющая силы Р₂;

P₂ sin α — горизонтальная составляющая силы Р₂;

2qa — равнодействующая равномерно распределенной нагрузки интенсивностью q (показана штриховой линией);

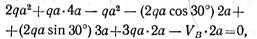
откуда V_B = 5,27qa;

или

откуда H_A=7qa

линия действия силы Р₂ cosα проходит через точку В и поэтому ее момент относительно точки В равен нулю

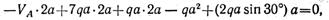
откуда V_A = 7qa.

Для определения реакций не было использовано урав­нение равновесия ΣP_iv=0. Если реакции определены верно, то сумма проекций на ось v всех сил, действую­щих на раму, должна быть равна нулю. Проектируя все силы на ось v, получаем:

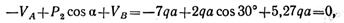
следовательно, опорные реакции определены верно.

Напомним, что сумма проекций сил, составляющих пару с моментом т, на любую ось равна нулю.

Контрольные вопросы и задания

1. Замените распределенную нагрузку сосредоточенной и опре­делите расстояние от точки приложения равнодействующей до опо­ры А (рис. 6.9).

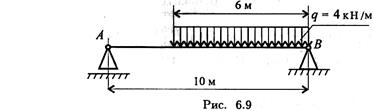
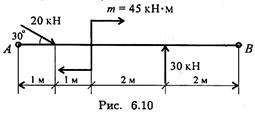
2. Рассчитайте величину суммарного момента сил системы от­носительно точки А (рис. 6.10).

3. Какую из форм уравнений равновесия целесообразно исполь­зовать при определении реакций в заделке?

4. Какую форму системы уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?

6. Определите вертикальную реакцию в заделке для балки, представленной на рис. 6.11.