Решение. Рассмотрим равновесие балки AB, к которой приложены как заданные, так и искомые силы.

Рассмотрим равновесие балки AB, к которой приложены как заданные, так и искомые силы.

На балку действуют равномерно распределенная на­грузка интенсивностью q, сила Р и сосредоточенный мо­мент т.

Освободим балку от связей и заменим их действие реакциями (рис. 1.19, б). Получили плоскую систему про­извольно расположенных сил.

Выбираем систему координат (см. рис. 1.19, б) и со­ставляем уравнения равновесия:

где q (a + b) — равнодействующая

равномерно распреде­ленной нагрузки интенсивностью q (на чертеже она показана штриховой ли­нией).

Подставив числовые значения, получим:

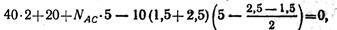
откуда N_AC = 16 кН;

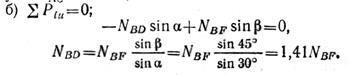
Напомним, что сумма проекций сил, образующих пару, на любую ось равна нулю;

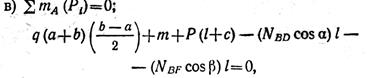
где N_BD cos α — вертикальная составляющая силы N_BD', N_BFcos β — вертикальная составляющая силы N_BF(линии действия горизонтальных состав­ляющих сил N_BDи N_BF проходят через точку А и поэтому их моменты относи­тельно точки А равны нулю). Подставляя числовые значения и учитывая, что N_BD= 1,41 N_BF, получаем:

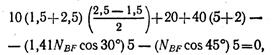
откуда N_BF = 33,1 кН.

Тогда N_BD = 1,41*33,1 = 46,7 кН.

Для определения усилий в стержнях не было исполь­зовано уравнение равновесия: ΣP_to= 0. Если усилия в стержнях определены верно, то сумма проекций на ось v всех сил, действующих на балку, должна быть равна нулю. Проектируя все силы на ось v, получаем:

следовательно, усилия в стержнях определены верно.

Пример 6. Для заданной плоской рамы (рис. 1.20, а) определить опорные реакции