Построение развёртки призмы.

Развёртки

Представим поверхность в виде тонкой и гибкой нерастяжимой плёнки. Некоторые поверхности постепенным изгибанием можно со­вместить с плоскостью так, что при этом не возникает ни разрывов, ни складок.

Поверхности, обладающими этим свойством, называются развер­тывающимися, а фигура, полученная в результате совмещения по­верхности с плоскостью, называется развёрткой поверхности.

Поверхность и её развёртку можно рассматривать как точечные множества, между элементами которых установлено взаимно одно­значное соответствие.

Это множество обладает следующими свойствами:

1. При развертывание поверхности на плоскость длины ли­ний, лежащих на ней, сохраняются;

2. Углы, образованные линиями на развёртке, и углы, между соответствующими линиями на поверхности, равны;

3. Замкнутая линия на поверхности и соответствующая ей ли­ния на развёртке ограничивают одинаковую площадь. Sразвёртки = Sсамой поверхности;

4. Прямой на поверхности соответствует прямая на развёртке;

5. Параллельным прямым на поверхности соответствуют параллельные на развёртке.

Если для поверхности нарушается одно из этих свойств, то поверхность относится к неразвёртывающимися.

К развёртывающим поверхностям относятся многогранники и следующие линейчатые поверхности: цилиндры, конусы, торсы.

В соответствие с этими развёртки поверхностей делятся на следующие виды:

1. точные – развёртки многогранников, прямых круговых цилиндров и конусов.

2. приближённые – развёртки развёртывающихся линейчатых поверхностей.

3. условные – развёртки неразвёртывающихся поверхностей.

Для построения развёрток многогранников применяют несколько способов.

1. Способ нормального сечения (для призм)

2. способ раскатки (для призм)

3. способ треугольников - треонгуляции (для пирамид, призматоидов)

Построение развёртки призмы.

Способ нормального сечения. Построение развёртки этим способом выполняется в следующей последовательности:

а) заданная призма пересекается плоскостью, перпендикулярно боковым рёбрам и строятся проекции многоугольника, лежащего в сечении (он называется нормальным сечением).

б) определяя натуральную величину многоугольного сечения.

в) определяется натуральная величина отрезков боковых рёбер призмы, лежащей выше и ниже нормального сечения.

г) на свободном поле чертежа проводится горизонтальная прямая, и на ней откладывают последовательно друг за другом натуральные величины сторон многоугольника нормального сечения.

д) через полученные точки проводят вертикальные прямые, на которых вверх откладывают натуральную величины отрезков боковых рёбер, лежащих выше нормального сечения, а вниз – лежащие ниже нормального сечения.

е) полученные точки соединяем отрезками прямых. Получилась развёртка боковой поверхности призмы. Если добавить к неё многоугольники оснований, получается полная развёртка призмы.

Построение развёртки пирамиды. Способ треугольников.

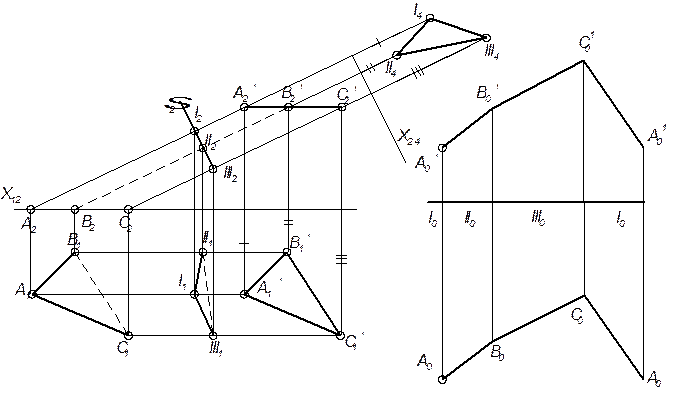
Рис. 1

Развёртка пирамиды осуществляется в следующем порядке:

а) определяют истинную величину всех ребер пирамиды методом прямоугольного треугольника, один катет которого равен отрезку S₂ 1 (разнице высот точек S и С), а другой – горизонтальным проекциям ребер (например для ребра SC, один катет равен отрезку S₂1, а другой катет – отрезку С₁=С₁S₁).

б) натуральная величина основания пирамиды спроецировалась на плоскость П₁.

Далее строят примыкающие один к другому треугольники с общей вершиной.

В треугольнике S₀А₀В₀, сторона S₀А₀=S₂A₂, сторона А₀В₀=А₁В₁.

Для построения полной развёртки пирамиды пристраивают основание пирамиды к одной из сторон боковых граней развёртки.

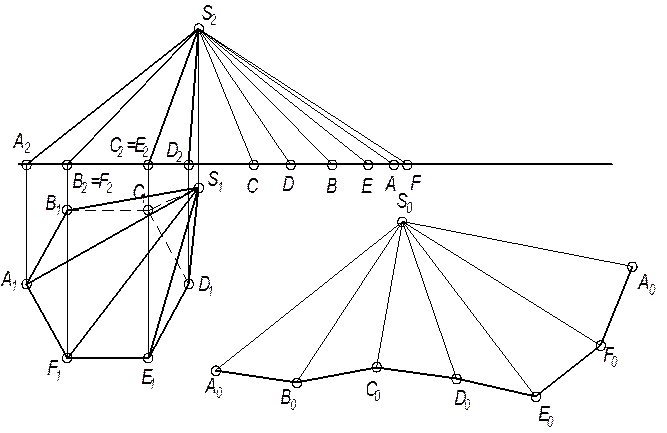
Рис. 2