Построение линии пересечения поверхности с плоскостью частного
Положения
В этом случае решение задачи значительно упрощается, т.к. нам сразу становится известна одна проекция линии пересечения. Она будет совпадать с вырожденной проекцией плоскости и лежать внутри очерка поверхности, поэтому остаётся построить лишь вторую проекцию искомой линии пересечения. Для этого нужно воспользоваться вспомогательными линиями, лежащими на поверхности (параллелями или образующими).
Пример.
Построить линию пересечения сферы с фронтально проецирующей плоскостью S.

3. Построение точки пересечения линии с поверхностью
Данная задача решается с помощью вспомогательной секущей поверхности.
Алгоритм решения:
1) заданную линию заключаем во вспомогательную поверхность Q.
2) строим линию пересечения вспомогательной поверхности Q с заданной поверхностью F.
3) построенная линия n и заданная линия  лежат на поверхности Q, а, значит, будут пересекаться. Точка их пересечения будет являться искомой точкой пересечения линии
лежат на поверхности Q, а, значит, будут пересекаться. Точка их пересечения будет являться искомой точкой пересечения линии  с поверхностью F.
с поверхностью F.
В качестве вспомогательной поверхности Q обычно используют:
1) плоскость (если заданная линия является прямой или плоской кривой);
2) проецирующая цилиндрическая поверхность (если заданная линия является пространственной кривой).
Пример.
Построить точку пересечения линии  с конической поверхностью общего вида
с конической поверхностью общего вида 
4. Взаимное пересечение поверхностей. Общий случай пересечения поверхностей
Линия пересечения двух поверхностей в общем случае является пространственной кривой, порядок которой = произведению порядков пересекающихся поверхностей.
Графически порядок кривой и поверхности определяется числом возможных точек пересечения с произвольной прямой.
Чтобы построить эту линию, необходимо воспользоваться вспомогательными секущими поверхностями.
Решение:
| 1)  2)
2)  3)
3) 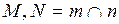
|
1. Обе заданные поверхности пересекаются вспомогательной поверхностью S. В качестве вспомогательной чаще всего используются плоскости, сферы или проецирующие цилиндрические поверхности.
2. Строятся линии пересечения вспомогательной поверхности S с каждой из заданных поверхностей.
3. Построенные линии m и n лежат на одной и той же поверхности S, а значит, пересекаются в точках M и N. Эти точки будут общими для трёх поверхностей:  , а значит, будут принадлежать искомой линии пересечения заданных поверхностей.
, а значит, будут принадлежать искомой линии пересечения заданных поверхностей.
Для построения других точек линии пересечения необходимо провести ещё несколько секущих поверхностей и выполнить аналогичные построения.
Найденные точки соединяются плавной линией по лекалу с учётом видимости. При этом нужно определить также и видимость очерковых линий поверхностей.
Выбор и расположение секущих вспомогательных поверхностей определяется следующими обстоятельствами:
1) желательно, чтобы линии пересечения вспомогательной поверхности с заданными были графически простыми линиями;
2) и чтобы они (эти линии) проецировались на какую-либо плоскость проекций без искажения.
5. Метод вспомогательных секущих плоскостей
Чаще всего в качестве вспомогательных используются проецирующие плоскости и плоскости уровня. Однако, в случае пересечения двух линейчатых поверхностей иногда используют плоскости общего положения.
Сложность решения задачи в многом определяется сложностью построения линий пересечения вспомогательной поверхности с заданной. Чем проще будут эти линии (прямые или окружности), тем проще будет решение задач.
Среди точек линии пересечения есть такие, которые выделяются своим особым положением среди остальных точек (самая верхняя и самая нижняя, крайняя правая и левая, точки – границы видимости и т.д.). Такие точки называются особыми или опорными, и строить их нужно в первую очередь.
Обычно эти точки находятся сразу без применения дополнительных построений. Остальные точки линии пересечения называются промежуточными, и все они строятся с помощью одного и того же приёма.
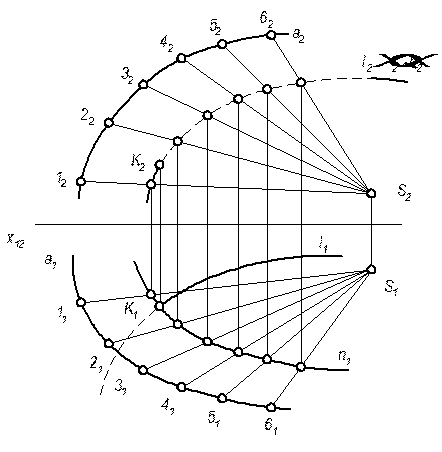
Пример.
Построить линию пересечения сферы с прямым круговым конусом.

| 1)  2)
2) 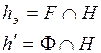 3)
3) 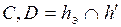 4)
4) 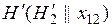 5)
5) 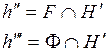 6)
6) 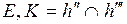
|
Дата добавления: 2015-10-26; просмотров: 1242;
