ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ ГАЗА МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ

Удельной теплоемкостью газа называется величина, численно равная количеству теплоты, которое необходимо сообщить единице массы газа, чтобы увеличить ее температуру на один градус.

Для газов эта величина зависит от условий, при которых проводится нагревание. Нагревание можно проводить при постоянном объеме или при постоянном давлении. Тогда получим соответствующие удельные теплоемкости: С_V -при постоянном объеме, C_Р – при постоянном давлении. При нагревании газа при постоянном объеме все количество теплоты идет только на увеличение внутренней энергии газа (С_VDT), при нагревании газа при постоянном давлении кроме теплоты, идущей на повышение внутренней энергии газа, необходимо еще количество теплоты, которое идет на совершение работы расширения газа (PDV ).

Непосредственное измерение С_P и С_V экспериментально затруднено, т. к. теплоемкость газа составляет ничтожную долю теплоемкости сосуда, заключающего газ, и поэтому измерение будет чрезвычайно неточно: проще измерить отношение величин .

Это отношение теплоемкостей g входит в уравнение Пуассона, описывающего адиабатические процессы Р₁V₁^g = Р₂V₂^g, и поэтому для определения его предлагается метод адиабатического расширения.

Отношение зависит только от числа степеней свободы молекул, из которых состоит газ, т. е. , гдеi – число степеней свободы.Численное значение различно для одноатомных газов и многоатомных. Соответственно, число степеней свободы для одноатомных газов i = 3, двухатомных i = 5, многоатомных i = 6. В настоящей работе определяется для воздуха (двухатомный газ).

Описание эксперимента

Метод определения , используемый в настоящей работе, основан назаконе адиабатического расширения газа. Адиабатическим называется процесс, происходящий без теплообмена с окружающей средой.

За характером процесса в опыте удобно проследить, ориентируясь на те изменения, которые будет претерпевать удельный объем, т. е. объем, занимаемый единицей массы газа.

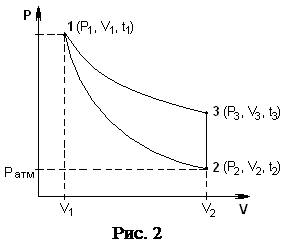
В стеклянный баллон Б (рис. 1) при помощи насоса Н накачивают воздух, создавая внутри баллона давление выше атмосферного. Это состояние будет соответствовать началу эксперимента, которое на графике характеризуется точкой 1 (рис. 2), а газ имеет параметры : V₁, Р₁, t₁.

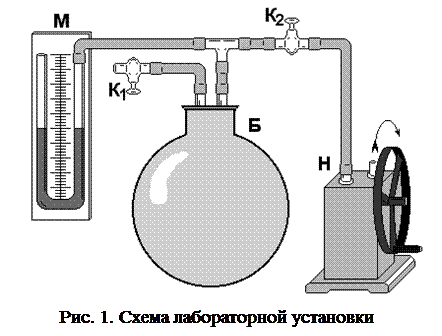
Быстрое расширение газа можно с достаточным приближением рассматривать как адиабатическое, поэтому, открывая кран А на короткое время, в течение которого давление внутри баллона достигает атмосферного, мы можем считать, что газ перейдет в новое состояние, характеризируемое величинами: V₂, Р₂, t₂, на графике точка 2 (рис. 2).

Температура газа (t₂) после адиабатического расширения будет меньше (t₀) окружающей. Параметры начального и конечного состояния газа связаны уравнением адиабаты:

Р₁V₁^g= Р₂V₂^g_­ (1)

через 3–5 минут газ нагревается до температуры окружающего воздуха (t₀). Поскольку при нагревании V₂ неизменно, то давление повысится до Р₃.

Новое состояние газа характеризируется параметрами: Р₃,V₂,t₃(t₃= t₀), см. на рис. 2. Сравнивая конечные состояния газа (рис. 2) в точке 3 с исходными, (точка 1) видим, что они находятся при одной температуре. Тогда по закону Бойля-Мариотта имеем:

Р₃V₂= Р₁V₁ (2)

Возведем уравнение (2) в степень g и разделим его почленно на уравнение (1):

Логарифмируя уравнение (3), находим g:

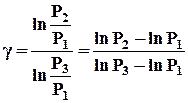(4)

Условия эксперимента позволяют упростить расчетную формулу следующим образом: обозначим давление в баллоне через Р₁, а разность уровней жидкости в манометре через Н, тогда:

Р₁= Р₂+ bН , (5)

где Р₂ – атмосферное давление;

b – коэффициент перехода от разностей уровней к давлению.

Для давления Р₃ разность уровней обозначим через h, тогда
Р₃= Р₂+ bh;

Выразим Р₂из уравнения (5) и подставим в (6), получим:

Р₃= Р₁ – b(H – h)

Наконец, подставляя Р₂ и Р₃ в уравнение (4), получим:

Величины и много меньше единицы. Тогда, используяприближенную формулу ln(1 – x)= – x , справедливо для малых x, получим:

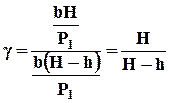(7)

Формула (7) является расчетной для определения g.