Преобразование уравнений
1)Уравнение Нернста-Планка.
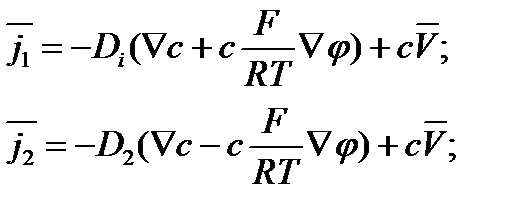
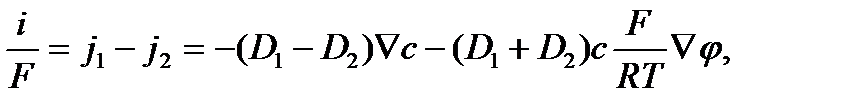 , ,
| (4.7) |
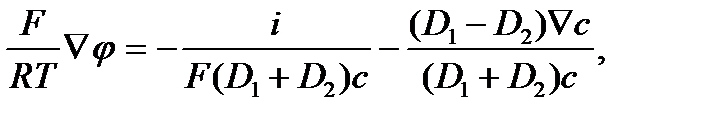 , ,
| (4.8) |
Подставляем в выражение с 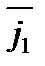 :
:

то есть:
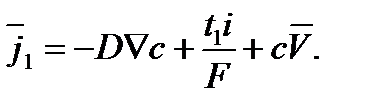 , ,
| (4.9) |
где  коэффициент диффузии электролита,
коэффициент диффузии электролита,  число переноса ионов сорта 1. Физический смысл: доля электрического заряда, который переносят ионы, при условии, что
число переноса ионов сорта 1. Физический смысл: доля электрического заряда, который переносят ионы, при условии, что  и скорость течения равны 0.
и скорость течения равны 0. 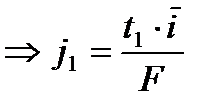
 , при
, при 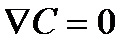 ,
, 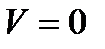 .
.
Если 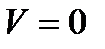 и
и 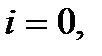 тогда
тогда 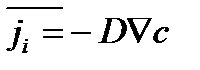 , т.е.
, т.е.  - это диффузия ионов 1 и 2 в одном направлении и с одинаковой скоростью.
- это диффузия ионов 1 и 2 в одном направлении и с одинаковой скоростью.
 - диффузионный потенциал.
- диффузионный потенциал.
Если  то в (4.9)
то в (4.9)
 , т.е.
, т.е. 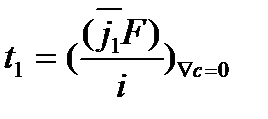 ,
, 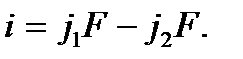
Число переноса показывает долю электричества, которая переносится ионами 1 при условии, что 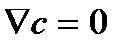 .
.
1. Уравнение Нернста-Планка и уравнение материального баланса.
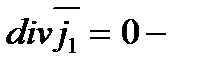 уравнение материального баланса.
уравнение материального баланса.
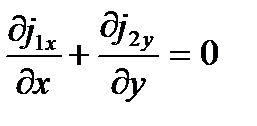
| (4.10) |
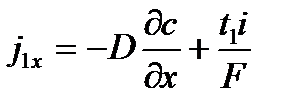
| (4.11) |
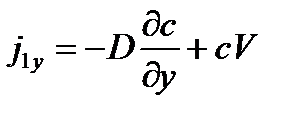
| (4.12) |
Подставляем в (4.10) и дифференцируем:
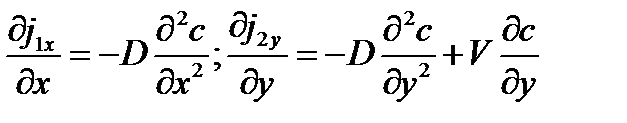 , т.е.:
, т.е.:
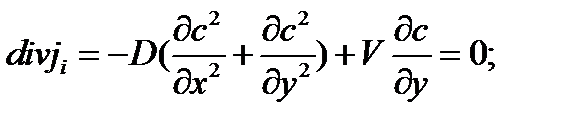
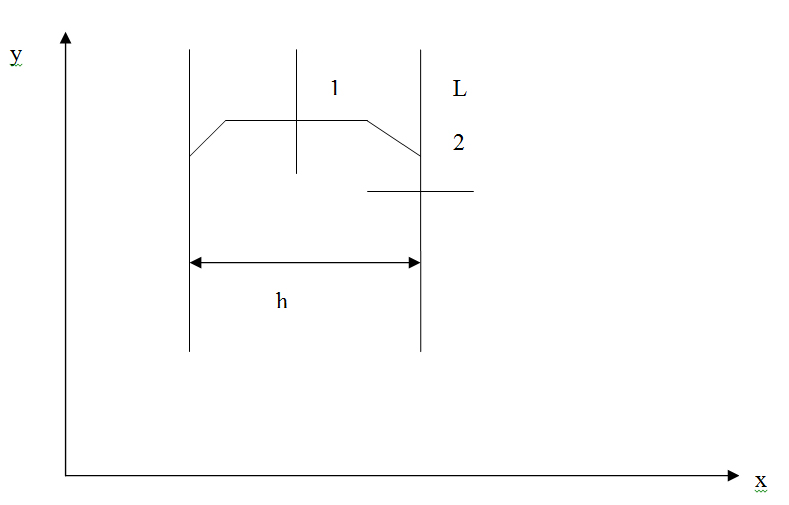
2. Оценка производных:
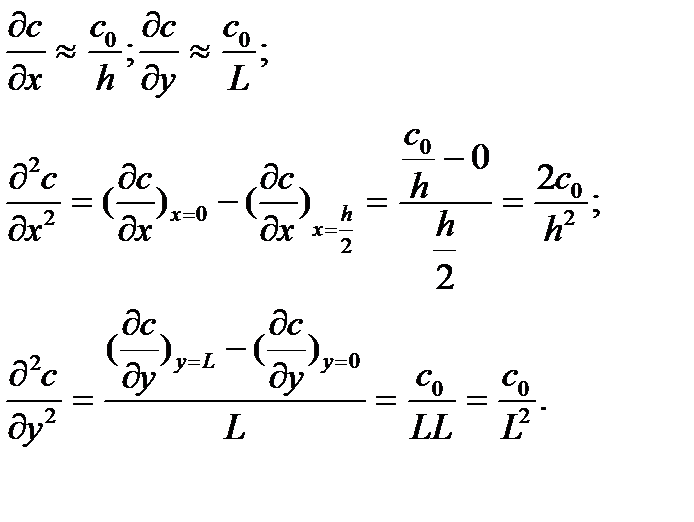
Так как 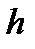 по меньшей мере на 2 порядка меньше чем
по меньшей мере на 2 порядка меньше чем 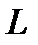 , то
, то  на 4 порядка больше чем
на 4 порядка больше чем 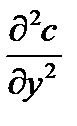 , этим слагаемым мы пренебрегаем.
, этим слагаемым мы пренебрегаем.

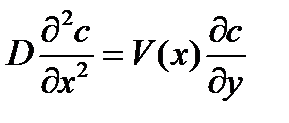 , ,
| (4.13) |
Это дифференциальное уравнение в частных производных – основное уравнение модели.
3. Граничные условия.

 где
где 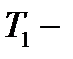 эффективное число переноса, которое показывает долю электричества, переносимую ионами 1 через мембрану в условиях, когда перенос осуществляется диффузией и миграцией.
эффективное число переноса, которое показывает долю электричества, переносимую ионами 1 через мембрану в условиях, когда перенос осуществляется диффузией и миграцией.
 , ,
| (4.14) |
Из (4.14) и (4.11) получаем:
При 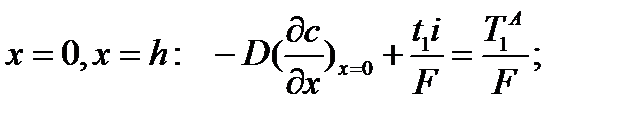
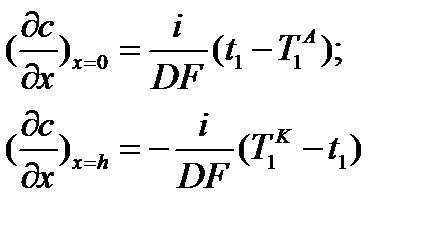 , ,
| (4.15) |
A, K – анионо- и катионообменная мембрана, 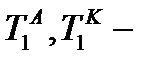 считаем известными.
считаем известными.
Второе граничное условие:
Значение скачков потенциала можно найти путем интегрирования уравнения (4.8) , представленные граничными условиями (4.5):
 , ,
| (4.16) |
Дата добавления: 2015-10-21; просмотров: 747;
