Определение ускорения точки В.
Запишем векторное уравнение: 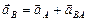 .
.
Вектор относительного ускорения 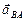 раскладываем на нормальную и касательную составляющие:
раскладываем на нормальную и касательную составляющие: 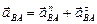 .
.
Нормальное относительное ускорение равно:
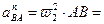
 .
.
Найдём отрезок, изображающий вектор ускорения 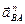 на плане:
на плане: 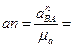
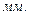
Продолжаем строить план ускорений. Вектор ускорения 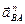 направлен параллельно АВ. Откладываем отрезок
направлен параллельно АВ. Откладываем отрезок  из точки
из точки 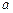 плана ускорений в указанном направлении от точки В к точке А.
плана ускорений в указанном направлении от точки В к точке А.
Вектор ускорения 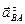 направлен перпендикулярно АВ. Проводим это направление из точки
направлен перпендикулярно АВ. Проводим это направление из точки 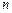 плана ускорений.
плана ускорений.
Вектор ускорения 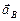 направлен параллельно оси x – x. Проводим это направление из полюса
направлен параллельно оси x – x. Проводим это направление из полюса 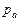 . Две прямые линии, проведённые из точек
. Две прямые линии, проведённые из точек 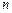 и
и 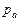 в указанных направлениях, пересекаются в точке
в указанных направлениях, пересекаются в точке 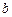 .
.
Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб 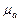 , получим:
, получим:
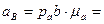
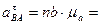
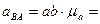
Дата добавления: 2015-10-21; просмотров: 549;
