Рациональные сечения при изгибе
 Определим рациональные сечения при изгибе, для этого сравним моменты сопротивления простейших сечений.
Определим рациональные сечения при изгибе, для этого сравним моменты сопротивления простейших сечений.
Осевой момент инерции прямоугольника (рис. 32.4, вывод формулы в лекции 25) равен
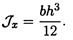
Осевой момент сопротивления прямоугольника
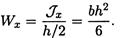
Сравним сопротивление изгибу двух прямоугольных сечений (рис. 32.5).
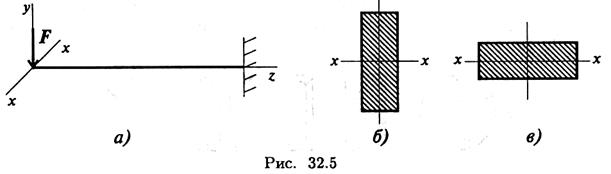

Вариант на рис. 32.5, б обладает большим сопротивлением изгибу при прочих равных условиях.
Осевой момент инерции круга (рис. 32.6) равен
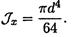
Осевой момент сопротивления круга
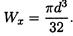
Все необходимые расчетные данные (площади, моменты инерции и сопротивления) стандартных сечений приводятся в таблицах стандартов (Приложение 1).
Для материалов, одинаково работающих на растяжение и сжатие, выбирают сечения, симметричные относительно оси, вокруг которой совершается изгиб (рис. 32.7).
Пример
Сравним моменты сопротивления двух сечений одинаковой площади: двутавра (рис. 32.7г) и круга (рис. 32.7а).
Двутавр № 10 имеет площадь 12 см2, осевой момент инерции 198см4, момент сопротивления 39,7см3.
Круг той же площади имеет диаметр 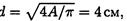 осевой
осевой
момент инерции Jx = 25,12см4, момент сопротивления Wx = 6,2см3.
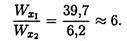
Сопротивление изгибу у двутавровой балки в шесть раз выше, чем у балки круглого сечения.
Из этого примера можно сделать вывод: сечения прямоугольные, квадратные, круглые и ромбовидные нерациональны (рис. 32.7а, б).
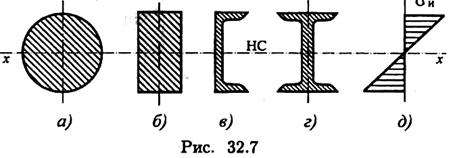
Для материалов, обладающих разной прочностью при растяжении и сжатии (хрупкие материалы обладают значительно большей прочностью на сжатие, чем на растяжение), выбирают асимметричные сечения тавр, рельс и др.
Дата добавления: 2015-09-07; просмотров: 1322;
