Решение. Определим опорные реакции;

Определим опорные реакции;

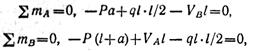
откуда

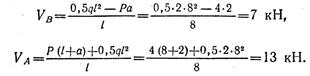
Составим прове­рочное уравнение:

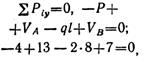
следовательно, реакции определены вер­но.

Балка имеет два участка I, II (рис. 2.54, а). На уча­стке I при измене­нии z от 0 до 1 м Q ^I_y = — Р = — 4 кН по­стоянна; М_x^I = Р_z = — 4z₁ — прямая ли­ния; при z = 0 М_x^I = 0; при z = 2 м М_x^I = — 4_*2= — 8 кН-м.

Для сечения на участке II при изме­нении z от 2 до 10 м

Q^l_y^l = — P+V_A — q(z — 2) = — 4 + 13 — 2 (z — 2) — прямая линия;

M_x" = P_z + V_A (z — 2) — 0,5q (z — 2)² = — 4z + 13 (z — 2) — (z — 2)² — парабола.

Найдем на участке II сечение, соответствующее экстремальному значению изгибающего момента: для этого приравняем нулю значение поперечной силы на этом участке:

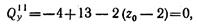
откуда z₀ = 6,5 м.

Подставляя в уравнение для М¹¹_х найденное значе­ние z₀, получаем:

приz₀ = 6,5 м М¹¹_х = М_тах = 12,25 кН-м; кроме того, при z = 2 м М¹¹_х = 8 кН-м, Q^ll_y = 9 кН; при z = 10 м М¹¹_х = 0, Q_v = — 7 кН. По этим значениям построе­ны эпюры попереч­ных сил и изгиба­ющих моментов (рис. 2.54, б, в).

Пример 5. Построить эпюры из­гибающих моментов и поперечных сил для балки, изобра­женной на рис. 2.55, а.