Решение. Определяем опорные реакции:
 |
Определяем опорные реакции:
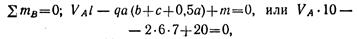
Откуда
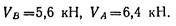
Составляем проверочное уравнение:
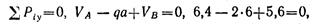
следовательно, опорные реакции определены верно.
Балка имеет три участка I, II, III (рис. 2.55, а): участок I — z = 0 — 6 м; участок II — z = 6 — 8 м; участок III – 2 = 8 — 10 м.
На участке I при изменении z от 0 до 6 м
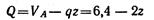-- уравнение прямой линии, наклоненной к оси балки;
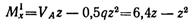-- уравнение параболы.
На участке II при изменении z от 6 до 8 м
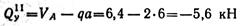-- уравнение прямой, параллельной оси балки;
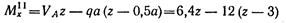-- уравнение прямой, наклоненной к оси балки.
На участке III при изменении z от 8 до 10 м
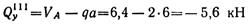-- уравнение прямой (такой же, как и для участка II);
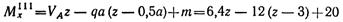-- уравнение прямой, наклоненной к оси балки.
Подставляя в уравнения поперечных сил и изгибающих моментов значения абсцисс z, соответствующие границам участков, получаем величины Qy и Мх в соответствующих сечениях:
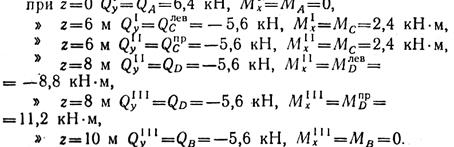
В сечении, где приложена сосредоточенная пара сил, имеется скачок в эпюре изгибающих моментов, равный величине момента пары т = 20 кН-м. Чтобы найти максимальное значение изгибающего момента на участке I, приравняем нулю значение поперечной силы на этом участке:
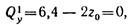
откуда z0 = 3,2 м.
Подставив это значение г0 в уравнение для MlX, получаем:
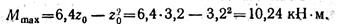
Следует иметь в виду, что наибольший изгибающий момент может не совпадать с аналитическим максимумом, как, в частности, оказалось в нашем случае.
Эпюры поперечных сил и изгибающих моментов построены на рис. 2.55,б, в.
Заметим, что при определении изгибающих моментов на участке III проще было рассматривать равновесие правой отсеченной части балки.
Пример 6. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.56, а.
 |
Решение
Определим опорные реакции:
откуда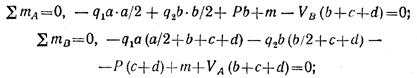 
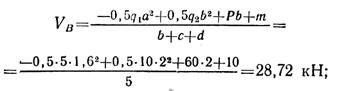
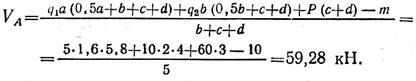
Составим проверочное уравнение:
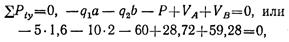
следовательно, реакции вычислены верно.
Балка имеет четыре участка I, II, III, IV (рис. 2.56, а).
Проводим сечение в пределах участка I (0 ≤ z ≤ 1,6 м) и, рассматривая равновесие левой отсеченной части, определяем аналитические выражения поперечной силы и изгибающегомомента на этом участке:
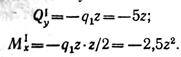
Поперечная сила изменяетсяпо линейному закону:
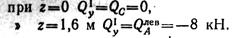
Изгибающий момент М1Х изменяется по закону квадратной параболы, параболу строим по двум точкам:
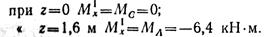
Аналогично, проводя сечения на участке II (1,6 м ≤ z ≤ 3,6 м) и рассматривая равновесие левой отсеченной части балки, получаем:
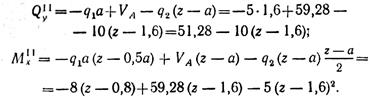
Поперечная сила на участке II, как и на участке I, изменяется по линейному закону:
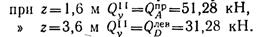
Изгибающий момент на участке II изменяется по закону квадратной параболы:
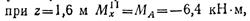
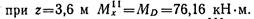
Проводим сечение на участке III и рассматриваем равновесие правой части, отсчитывая абсциссы от точки В (1,8 м < z1 < 3 м).
К правой отсеченной части балки приложено меньше внешних сил, чем к левой, поэтому составление аналитических выражений для поперечной силы и изгибающего момента будет проще:
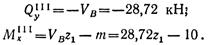
Поперечная сила на участке III постоянна. Изгибающий момент изменяется по линейному закону:
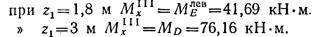
Проводя сечение на участке IV, так же рассматриваем равновесие правой отсеченной части (0 ≤ z1 < 1,8 м):
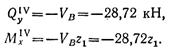
Эпюра поперечных сил изображается прямой, параллельной оси балки, как и на третьем участке. Эпюра изгибающих моментов имеет вид наклонной прямой:
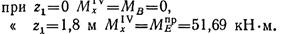
По полученным данным на рис. 2.56, б, в построены эпюры поперечных сил и изгибающих моментов.
Контрольные вопросы и задания
1. Если эпюра поперечной силы ограничена наклонной прямой, как выглядит эпюра изгибающего момента?
2. Как определить положение экстремального значения изгибающего момента при действии распределенной нагрузки на участке балки?
3. Распределенная нагрузка направлена вверх. Как выглядит парабола, очерчивающая эпюру изгибающих моментов вдоль оси бруса?
4. Определите координату z, в которой поперечная сила равна нулю (рис. 31.4).
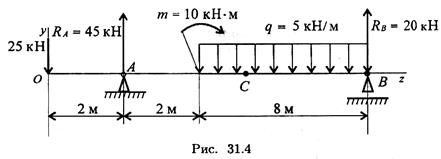
5. Определите величину изгибающего момента в точке С (z = = 5 м), используя схему рис. 31.4.
Дата добавления: 2015-09-07; просмотров: 1251;