Решение. 5. Определение реакций в опорах.

5. Определение реакций в опорах.

Уравнения равновесия:

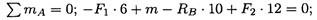
Реакция в опоре направлена в обратную сторону.

Проверка: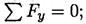

Реакции определены верно.

2. Для упрощения расчетов при построении эпюр поперечных сил и изгибающих моментов можно провести расчет по характерным точкам без составления уравнений.

Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр.

Участок 1 (от точки А до точки С).

В точке А приложена реакция Ra, направленная вниз. Попереч­ная сила на участке постоянна: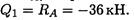

Момент в точке А равен нулю.

Точка С (слева). Приложена внешняя сила F₁ = 35кН, направ­ленная вверх, — здесь возникнет скачок вверх на величину 35 кН. Момент в точке С (слева) может быть рассчитан по известной зави­симости

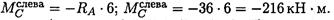
Участок 2 (от точки С справа до точки В).

Поперечная сила в точке С (справа) равна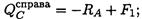

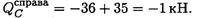
В точке С приложена внешняя пара сил с моментом 80кН-м, следовательно, здесь проявляется скачок на величину приложенного момента:

.

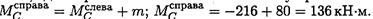
Поперечная сила на втором участке постоянна: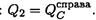

Момент в точке В определяется по зависимости М_в = -Ra * 10 + F₁ * 4 + m; М_в = -36 • 10 + 35 • 4 + 80 = -140кН-м.

Справа и слева от точки В момент имеет одинаковые значения.

Участок 3 (от точки В (справа) до точки D).

В точке В приложена внешняя сила R_B. Здесь появляется ска­чок на величину 71 кН,

Q_B = — 1 + 71 = 70 кН.

Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т. к. здесь не приложена внешняя пара сил: M_D = 0.

Рассмотрение поперечных сил и изгибающих моментов можно было провести слева направо или справа налево.

По полученным значениям сил и моментов строим эпюры (эпю­ры под схемой вала, рис. 30.4).

Контрольные вопросы и задания

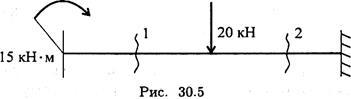
1. Определите величины поперечных сил в сечении 1 и в сече­нии 2 (рис. 30.5).

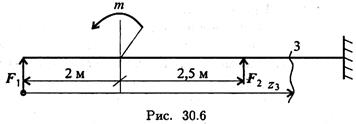
1. Напишите формулу для расчета изгибающего момента в се­чении 3 (рис. 30.6).

1. Из представленных эпюр выберете эпюру поперечной силы для изображенной балки (рис. 30.7).