Решение. Определяем опорные реакции VA и VB:

Определяем опорные реакции V_A и V_B:

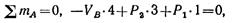
откуда

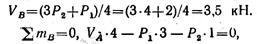
Откуда

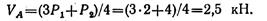
Составляем проверочное уравнение:

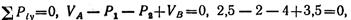
следовательно, опорные реакции определены верно.

Валка имеет три участка I, II, III (см. рис. 2.53, а): участок I — от опоры А до силы Р₁ (0 < z < l м), уча­сток II — от силы Р₁ до силы Р₂ (1 м << z < 3 м), участок III — от силы Р₂ до опоры В. На этом участке абсциссу удобнее отсчитывать не слева, а справа, т. е. от опоры В ( 0 < z₁ < 1 м).

Поперечная сила в произвольном сече­нии участка I

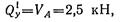
в произвольном сече­нии участка II

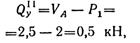
в произвольном сечении участка III

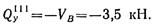
Если рассматривать левую отсеченную часть балки, то получим то же самое значение поперечной силы:

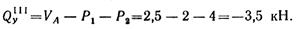
В последнем случае вычисления оказались более гро­моздкими, так как к левой части балки приложено три силы, а к правой — только одна. В пределах каждого участка поперечная сила постоян­на. По вычисленным значениям с соблюдением правила знаков эпюра Q_y построена на рис. 2.53, б. Эпюра имеет скачки под сосредоточенными силами V_A, P₁, Р₂, V_B, величина и направление скачка соответствуют величине и направлению внешней силы.

Переходим к построению эпюры изгибающих момен­тов. Берем сечение в пределах участка /; слева от него расположена одна сила — опорная реакция V_A. Изгибаю­щий момент в произвольном сечении участка I

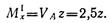
Полученное выражение является уравнением прямой, поэтому для построения эпюры моментов на этом участке достаточно найти ординаты двух точек:

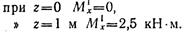
Значение ординаты М_х = 2,5 кН-м в выбранном мас­штабе откладываем вверх под точкой приложения силы P_v. Для определения изгибающего момента на участке II также рассматриваем равновесие левой отсе­ченной части балки:

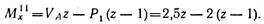
Полученное выражение является уравнением прямой.

Для построения эпюры изгибающих моментов на участке II нужно определить ординаты в двух точках:

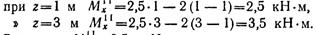
Значение M_x^II = 3,5 кН-м откладываем вверх под силой Р₂ и соединяем с уже построенной ординатой в сечении под силой P₁.

На участке III целесообразно рассмотреть правую часть балки, так как к ней приложено меньше сил, чем к левой:

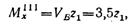
где z₁ отчитывается от опоры В и изменяется в преде­лах от 0 до 1 м;

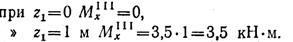
Под силой Р₂ значение M_x^II = M_x^11I, что подтверждает правильность решения.

Эпюра изгибающих моментов изображена на рис. 2.53, в.

Пример 4. На балку действуют сосредоточенные силы и мо­мент (рис. 30.1). Построить эпюры поперечных сил и изгибающих моментов.