Решение. Центр тяжести лежит на оси Оу, так как она является осью сим­метрии сечения

Центр тяжести лежит на оси Оу, так как она является осью сим­метрии сечения. Раз­бив сечение на два прямоугольника I (160 x 100) иII(140 x 80) и выбрав вспомогательную ось и, определим коорди­нату центра тяжести v₀ по формуле

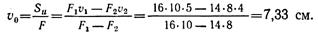
Оси Ох и Оу — главные центральные оси сечения (Оу — ось симметрии, ось Ох проходит через центр тя­жести сечения и перпендикулярна к Оу).

Вычислим главные моменты инерции сечения J_x и J_y:

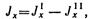
где

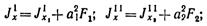
здесь

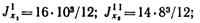
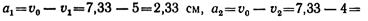
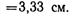
Тогда

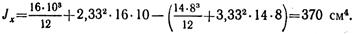
Ось Оу является центральной осью для прямоуголь­ников 1 и 11. Следовательно,

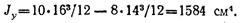
Для проверки правильности решения можно разбить сечение на прямоугольники другим способом и вновь произвести расчет. Со­впадение результатов явится подтверждением их правильности.

Пример 5. Вы­числить главные цент­ральные моменты инер­ции сечения (рис. 2.47).