Решение. Сечение имеет две оси симметрии, которые и являются его главными центральными осями.
Сечение имеет две оси симметрии, которые и являются его главными центральными осями.
Разбиваем сечение на два прямоугольника с b * h = 140 x 8 и два прокатных швеллера. Для швеллера № 16 из таблицы ГОСТ 8240 – 72 имеем JX1 = Jx = 747 см4; Jy1 = 63,3 см9, F1 = 18,1см2, z0 = 1,8см.
Вычислим Jx и Jy:
Пример 6. Определить положение главных центральных осей и вычислить главные центральные моменты инерции заданного сечения (рис. 2.48).
Решение
Заданное сечение разбиваем на прокатные профили: швеллер I и два двутавра II. Геометрические характеристики швеллера и двутавра берем из таблиц прокатной стали ГОСТ 8240—72 и ГОСТ 8239 — 72.
Для швеллера № 20 JXl = 113 см4 (в таблице Jy); Jy1 = 1520 см4 (в таблице Jx); F1 = 23,4 см2; г0 = 2,07 см.
Для двутавра №18 Jx2 = 1330 см4 (в таблице Jx); Jy2 = 94,6 см4 (в таблице Jy); F2 = 23,8 см2.
Одной из главных осей является ось симметрии Оу, другая главная ось Ох проходит через центр тяжести сечения перпендикулярно к первой.
Выбираем вспомогательную ось и и определяем координату v0:
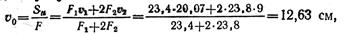
где v1 = 180 + 20,7 = 200,7 мм и v2 = 180/2 = 90 мм. Вычисляем Jx и Jу:
 |
Контрольные вопросы и задания
1. Диаметр сплошного вала увеличили в 2 раза. Во сколько раз увеличатся осевые моменты инерции?
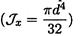
2. Осевые моменты сечения равны соответственно Jx = 2,5 мм4 и Jy = 6,5мм. Определите полярный момент сечения.
3. Осевой момент инерции кольца относительно оси Ох Jx = 4 см4. Определите величину Jp.
4. В каком случае Jx наименьшее (рис. 25.7)?
5. Какая из приведенных формул для определения Jx подойдет для сечения, изображенного на рис. 25.8?
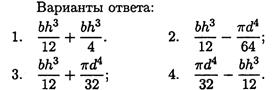
6. Момент инерции швеллера № 10 относительно главной центральной оси JXQ = 174см4; площадь поперечного сечения 10,9 см2.
Определите осевой момент инерции относительно оси, проходящей через основание швеллера (рис. 25.9).
7. Сравнить полярные моменты инерции двух сечений, имеющих практически одинаковые площади (рис. 25.10).
8. Сравнить осевые моменты инерции относительно оси Ох прямоугольника и квадрата, имеющих одинаковые площади (рис. 25.11).
 |
Дата добавления: 2015-09-07; просмотров: 1442;