Исходные данные для расчета надежности
| Элемент | Вероятность безотказной работы Р | ||
| Вариант | |||
| Первый | 0,45 | 0,75 | 0,9 |
| Второй | 0,65 | 0,6 | 0,95 |
| Третий | 0,9 | 0,7 | 0,2 |
| Четвертый | 0,3 | 0,85 | 0,8 |
| Пятый | 0,9 | 0,8 | 0,7 |
| Шестой | 0,9 | 0,9 | 0,6 |
| Седьмой | 0,95 | 0,55 | 0,75 |
| Восьмой (резервный) | 0,95 | 0,9 | 0,9 |

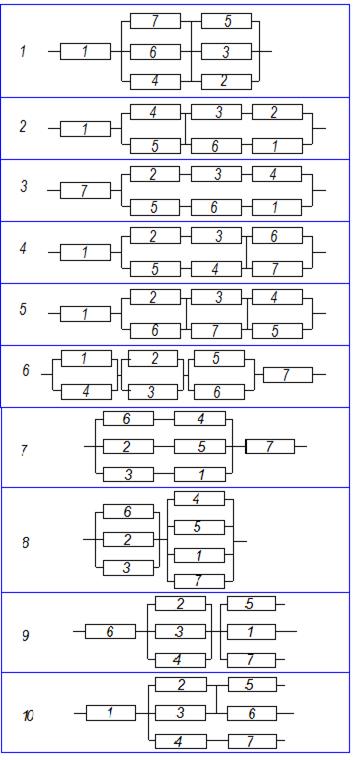
Рис. 3. Схемы для расчета надежности
Задание 3.Рассчитать вероятность безотказной работысложной системы для схем.
На практике встречаются системы, для описания которых параллельное или последовательное соединение не годится. Рассмотрим в качестве примера систему, изображенную на рис. 4.

Рис. 4. Система со сложным соединением элементов
В данной системе отказ элемента А нарушает сразу два пути – АС и АД. Таким образом, это соединение не является параллельным. Последовательным такое соединение назвать также нельзя: в случае отказа элемента С система остается работоспособной.
Для определения вероятности безотказной работы системы или надежности ее функционирования используют несколько методов. Здесь принят метод прямого перебора. Метод состоит в том, что рассматриваются все возможные способы появления отказов, т. е. не отказал ни один элемент, отказал один элемент, два и т. д.
В системе, изображенной на рис. 4, элементы имеют следующие вероятности безотказной работы:
Р(А) = 0,9; Р(В) = 0,8;
Р(С) = 0,6; Р(Д) = 0,7.
Здесь А – событие «элемент А работает безотказно»; тогда Ā – событие «элемент А отказал». Аналогично определяются события для всех остальных элементов. Затем вычисляется вероятность состояния системы для каждого способа появления отказа. Результаты записываются в табл. 3.
Таблица 3
Дата добавления: 2015-09-07; просмотров: 1882;
