Математичний опис динаміки руху вагонів на сортувальній гірці.
Розглядаючи окремий вагон як матеріальну точку з масою m, яка зосереджена в центрі ваги вагона і прикладеними до неї діючими зовнішніми силами (рис. 1.1), можна записати:
F - W = ma,
або у питомих силах
,
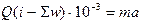де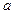 
- прискорення руху, м/с2;
і - уклон ділянки, на якій розташований вагон, ‰;
Sw - загальна величина усіх діючих сил опору руху в окремий момент, кгс/тс.
Зважаючи, що Q = mg, отримаємо
,
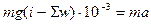звідки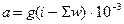 
, (1.8)
де g - прискорення вільного падіння, g = 9.81 м/с2 .
У диференційній формі прискорення а визначається
,
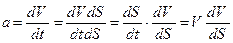де V- миттєва швидкість вагона, як матеріальної точки.
Підставляючи останнє в (1.8), отримаємо
,
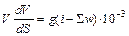або, поділяючи перемінні, дістанемо
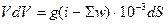. (1.9)
Диференційне рівняння (1.9) описує рух на похилій площині тіла, як матеріальної точки. Вагон у стані руху являє собою складну систему, яка містить елементи (колісні пари), що обертаються. Енергія обертального руху колісних пар впливає на процес поступального руху вагона.
Загальна енергія вагона Ек в окремий момент часу складається з кінетичної енергії поступального руху і енергії обертального руху колісних пар вагонів, тобто
.
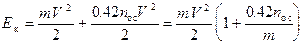де V- миттєва швидкість поступального руху;
nос- кількість осей вагона;
Питома (на одиницю ваги вагона) енергія становить
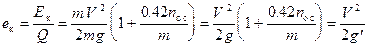. (1.10)
Величина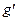 
в (1.10) являє собою приведене прискорення вільного падіння з урахуванням енергетичного впливу маси колісних пар, що обертаються, і визначається
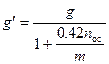, (1.11)
де m- маса вагона, т.
Таким чином, диференційне рівняння ( 1.9) для опису руху вагона як системи можна записати:
.
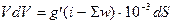Фізичне рівняння руху вагона можна отримати шляхом інтегрування останнього:
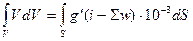. (1.12)
Інтегрування (1.12) в явному вигляді визнано неможливим. Достатньо точне для виконання інженерних розрахунків рішення можна отримати, якщо на елементарному переміщенні DS £ 10 м розглядати питомі сили як сталі величини.
В результаті, рівняння руху вагона буде мати вигляд
,
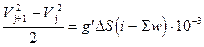звідки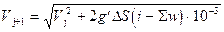 
. (1.13)
З допомогою виразу (1.13), як рекурентного, можливо розрахувати швидкість вагона в кінці кожної з послідовних ділянок DS маршрута, і отримати залежність V=f(S). При відносно малих DS ( не більше 5 м) тривалість скочування вагона t на кожному кроці можна визначити через середню швидкість, тобто
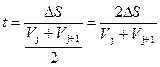. (1.14)
Підсумовуючи величини t на послідовних ділянках DS
Tj+1 = Tj + tj,j+1 , (1.15)
можна отримати залежність T = f(S).
Дата добавления: 2015-10-19; просмотров: 530;