Молекулярно-кинетическая теория идеальных газов

При рассмотрении газообразного вещества часто применяют модель идеального газа, в которой не учитывают:

¾ собственный объем молекул газа по сравнению с объемом резервуара;

¾ пренебрегают энергией взаимодействия молекул;

¾ считают столкновения молекул газа между собой и со стенками сосуда абсолютно упругими.

Для изучения свойств газа его обычно ограничивают сосудом с заданным объемом V. Газ в таком сосуде оказывает давление на стенки р (малые силы отдельных ударов молекул складываются в практически постоянную силу давления на стенку), которое, как показывает опыт, прямо пропорционально концентрации молекул, т. е. их количеству в единице объема и средней кинетической энергии поступательного движения молекул 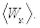Точный анализ приводит к следующему соотношению

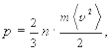(5.3)

где m ¾ масса молекулы, или

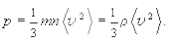(5.4)

Выражение (5.3) или (5.4) носит название основного уравнения молекулярно-кинетической теории идеального газа. Это уравнение связывает макроскопический параметр (давление) с микроскопическими параметрами молекул газа. В частности мы встречаемся с 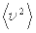¾средним значением квадрата скорости молекул. Усреднение необходимо, так как молекулы газа движутся хаотично. Как показывает опыт скорость их движения имеет определенное распределение, установленное Дж. Максвеллом в 1859 году и носящее его имя.

Перепишем уравнение (5.2) для средней кинетической энергии поступательного (i = 3) движения молекул в виде

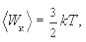(5.5)

тогда с учетом (5.3) имеем

р = nkT. (5.6)

Так как для смеси идеальных газов n₁ + n₂ + ... + n_n = n, то

р = р₁ + р₂ + … + р_n. (5.7)

В результате получим так называемый закон Дальтона: давление смеси идеальных газов на стенки сосуда равно сумме давлений ее отдельных компонент (парциальных давлений).

Следствием основного уравнения молекулярно-кинетической теории газов (5.4) является уравнение Клапейрона-Менделеева:

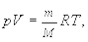(5.8)

где р ¾ давление газа, m ¾ его масса, V ¾ объем, М ¾ молярная масса, Т ¾ абсолютная температура (К) и R ¾ газовая постоянная.

На основании закона Авогадро можно показать, что один моль любого газа при нормальных условиях (р₀ = 1,013 × 10⁵ Па, Т₀ = 273,15 К) занимает одинаковый объем V_м =22,41 × 10^-3 м³/моль. Таким образом, имеем

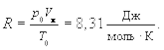
Частными случаями уравнения Клапейрона-Менделеева являются известные законы Бойля-Мариотта, Гей-Люссака и Шарля.