Задача 6.
Для решения задач теплопроводности с неизменяющимися граничными условиями третьего рода получено уравнение, позволяющее рассчитывать одновременное температурное поле в неограниченных плоских пластинах. При нагревании пластины с двух сторон используется формула (17.13) [3].
При одностороннем нагревании плиты толщиной δ в течении τ мин температура на расстоянии χ от необогреваемой поверхности рассчитывается по формуле
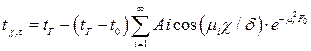 ,
,
где tг – температура греющей среды, 0С; t0 – начальная температура плиты, 0С. Аi = 2sinμi/(μi + sinμicosμi) – коэффициент; μi – корень характеристического уравнения; F0 = ατ/δ2 – число Фурье; χ = δ – s – расстояние от начала координат до заданной изотермической поверхности в плите, м.
Для случая, когда F0 ≥ 0,25, можно ограничиться только одним первым членом ряда. Если F0 < 0,25, то нужно взять сумму трех первых членов ряда.
Значение μ1, μ2, μ3 в зависимости от величины числа Био (Bi = αδ/λ) приведены в приложении XXX [4] или табл. 17.1[3]. При расчете Аi следует иметь ввиду, что значение μi выражается в радианах.
Коэффициенты А1, А2, А3 в зависимости от величины числа Био приведены в приложении XXXI [4].
При одностороннем нагревании на необогреваемой поверхности плиты перекрытия χ = 0, а на обогреваемой поверхности χ = δ.
При нагревании полуограниченного тела в течении τ мин температура на расстоянии χ = s от обогреваемой поверхности рассчитывается по формул 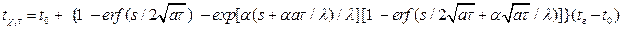
где erfА – функция Крампа. Значения функции в зависимости от величины аргумента А даны в приложении ХХIХ [4] или таб. 17.3 [3].
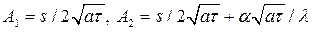
Дата добавления: 2015-10-19; просмотров: 872;
