Задача 5.
В теории теплообмена при решении задач теплопроводности известными могут быть: температура на внешней поверхности тела, плотность теплового потока на поверхности тела, температура среды, омывающей поверхность тела, и закон теплообмена между средой и поверхностью тела (коэффициент теплоотдачи).Первый тип задач называют задачами с граничными условиями 1 рода. Второй – задачами с граничными условиями 2 рода. Третий – задачами с граничными условиями 3 рода.
Исходные данные в рассматриваемый период могут изменяться или иметь постоянные значения. В соответствии с этим граничные условия называют изменяющимися или постоянными. Во время пожара, как правило, температура среды и коэффициент теплоотдачи имеют переменные значения.
Задачи теплопроводности с изменяющимися граничными условиями 3 рода наиболее просто решаются методом конечных разностей. Суть метода изложена в
§ 16.3 [3] и 16.8[3]. Графическое решение представляет собой приближенное изображение температурного поля в плите для каждого расчетного момента времени τ (τ = ίΔτ) в координатах χ, t. Данные по температуре греющей среды и условиям теплообмена на поверхности тела графически изображаются точкой (при изменяющихся во времени граничных условиях – точками) с абсциссой λ/α1 и ординатой tг с обогреваемой стороны и абсциссой λ/α2 и ординатой t0 с необогреваемой стороны плиты. Оси абсцисс перпендикулярны внешним поверхностям плиты и направлены от поверхностей в сторону среды. Начало отсчета абсцисс (χ = 0) находится на внешних поверхностях плиты. Масштаб при изображении толщины стенки и граничных условий одинаков.
В примере 12.25[4] дана методика решения задачи.
Важно правильно выбрать расчетный интервал времени Δτ и толщину расчетного слоя Δχ.
При графическом решении
Δχ = 2λ / α1max,
где α1max – максимальное значение коэффициента теплоотдачи на обогреваемой поверхности за период нагревания (τ = 30 мин), Вт/(м2∙0С)
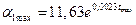 ,
,
где tmax – максимальное значение температуры среды за время пожара по результатам расчета задачи 4 контрольной работы (см. график изменения температуры среды под перекрытием), 0С.
Перекрытие условно разбивается на n слоев
n = δ/Δχ.
Если n получается не целым числом, то его следует округлить в большую сторону. После округления уточнить толщину расчетного слоя. (В случае, если n получается меньше 3, число расчетных слоев принимают равным 3)
Δχ = δ/n.
Это значение Δχ следует в дальнейшем использовать при решении задачи.
Интервал времени, через который выполняется каждый последующий расчет температуры греющей среды и температурного поля
Δτ = Δχ2/2α.
(Удобно использовать единицу времени – мин). Используя график изменения температуры под перекрытием (см. решение задачи 4), выписать значения температуры среды через полученный расчетом интервал времени Δτ вплоть до 30 мин (с точностью Δτ). Рассчитать значения коэффициента теплоотдачи с соответствии с температурой среды для каждого времени по формуле
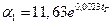
и результаты расчетов занести в таблицу:
| τ, мин | tг,0С | α1,Вт/(м2∙0С) | λ/α1,м | α2,Вт/(м2∙0С) | λ/α2,м |
| Δτ | |
| 2 Δτ | |
| ...... | |
| l Δτ | |
Заполнив графы 1, 2, 3, 4, можно приступить к решению задачи. Графическое решение целесообразно выполнять на миллиметровой бумаге. Графы 5 и 6 заполняются после того, как в ходе решения задачи будет установлено, что температура на внешней (необогреваемой) поверхности плиты перекрытия стала выше температуры окружающего воздуха (см. пример 12.25 [4], п.13). Значение α2 рассчитывается по предложенным в указанной литературе формулам.
Основой для графического расчета является формула
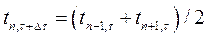 ,
,
где 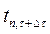 – температура в расчетном слое для расчетного момента времени
– температура в расчетном слое для расчетного момента времени 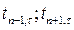 – температура в слое, предыдущем расчетному, для предыдущего момента времени
– температура в слое, предыдущем расчетному, для предыдущего момента времени 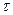 ;
; 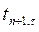 – температура в слое, последующем за расчетным, для предыдущего расчетному момента времени
– температура в слое, последующем за расчетным, для предыдущего расчетному момента времени 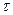 .
.
Значения 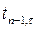 и
и 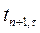 известны из ранее выполненных расчетов или даны по условию. Из формулы видно, что слагаемые должны быть одного временного порядка.
известны из ранее выполненных расчетов или даны по условию. Из формулы видно, что слагаемые должны быть одного временного порядка.
Алгоритм решения задачи
1. Выпишите максимальное значение температуры среды (для 30 мин) под перекрытием над факелом при пожаре в помещении, полученное расчетом при решении задачи 2.1.
2. Рассчитайте максимальное значение коэффициента теплоотдачи на поверхности плиты со стороны пожара.
3. Установите максимальную толщину расчетного слоя Δχ.
4. Установите максимальный расчетный интервал времени Δτ.
5. По графику изменения температуры среды над факелом под перекрытием (из решения задачи 2.1) определите температуру среды через Δτ, 2Δτ, 3Δτ, ...., 30 мин и запишите.
6. Рассчитайте значения коэффициента теплоотдачи α1 на поверхности плиты со стороны пожара для времени Δτ, 2Δτ, ...., 30 мин.
7. Рассчитайте величину абсциссы λ/α, направляющей точки для времени Δτ, 2Δτ, ...., 30 мин.
8. Начертите разрез плиты и разделите на n расчетных слоев толщиной Δχ каждый. Проведите осевые линии слева и справа за границами плиты на расстоянии Δχ/2 от ее поверхностей. Пронумеруйте осевые линии слева направо N, I, II, III, ..., М (оси N и M проходят вне плиты). По оси ординат выберите масштаб температуры.
9. Зафиксируйте на плоскости в координатах λ/α1 (абсцисса) t (ордината) положение направляющей точки А (А1, а2, А3, ...) для каждого расчетного момента времени τ (Δτ, 2Δτ, ...., 30 мин). Ордината точки соответствует температуре среды в расчетное время, а абсцисса равна отрезку λ/α1 для этого же времени.
10. Рассчитайте графически температурное поле в плите. Расчет ведется последовательно для времени Δτ, 2Δτ, .... через интервал времени Δτ.
11. На графике изобразите начальное температурное поле в плите, на каждой осевой (0, I, II, ...) отложите отрезок, соответствующий в масштабе начальной температуре в плоскостях, проходящих через осевые. На вершине каждого отрезка укажите порядок расчетного интервала времени. (Для начального времени 0). По условию задачи при τ = 0 температура по всему сечению плиты равна t0. Начальное температурное поле в плите изобразится прямой (0,0,0,...), параллельной оси абсцисс.
12. Соедините отрезком (0,0) значение температуры на осевой N для времени τ = 0 со значением температуры на осевой II для этого же времени (τ = 0). Точка пересечения отрезка (0,0) с осью I отсекает ординату, соответствующую значению температуры на этой оси для времени Δτ. Точку пересечения на оси I обозначьте индексом I. Индекс будет указывать порядок расчетного интервала времени. Соедините отрезком (0,0) значение температуры на осевой I для времени τ = 0 со значением температуры на осевой III для этого же времени. Точка пересечения отрезка с осью II отсекает ординату, соответствующую значению температуры на оси II для первого расчетного интервала времени Δτ. Точку пересечения на оси II обозначьте индексом I. Индекс имеет тот же смысл, что и ранее. Аналогично определите температуру для времени Δτ на осях III, ... . Завершается расчет температурного поля для времени Δτ определением температуры на оси N. Для этого соедините точку I на оси I с направляющей точкой I; точке пересечения отрезка (I, I) с осью N присвойте индекс I.
Ломанная I-I-I... приближенно соответствует температурному полю в плите для времени Δτ. Температура на осевых I, II, III, ... равна начальной.
Аналогично устанавливается температурное поле в плите для времени 2Δτ (3Δτ, ..., 30 мин). Основой для решения служат результаты расчета температурного поля в плите для времени Δτ (времени предыдущего рассматриваемому моменту). На ломанной проставляйте индексы, указывающие порядок расчетного интервала времени. Верхняя ломанная должна иметь индекс одного порядка. Каждый расчет начинайте с определения температуры на осевой I и завершайте определением температуры на осевой N (слева от плиты).
Дата добавления: 2015-10-19; просмотров: 1130;
