Убытки из-за дефицита запасов

Оценка потерь из-за отсутствия запасов достаточно сложная задача и требует анализа всех - возможных сценариев развития событий. Для предотвращения данных убытков на складе создают резервный запас. Резервный запас - это дополнительное количество запасов на складе для снижения вероятности дефицита запасов вследствие непредвиденной задержки времени поставки или превышения ожидаемой потребности в запасах за время поставки.

Перед тем как рассматривать резервные запасы, мы определим, при достижении какого порога будут сделаны заказы на восполнение запасов. Предположим, что спрос на товарно-материальные ценности известен абсолютно точно, но проходит 5 дней, прежде чем заказ будет получен.

Используя формулу наиболее экономичного размера заказа, мы обнаружили, что для нашей фирмы заказ был 200 ед., в результате чего заказ размещается каждые 10 дней. Если расход устойчив, то фирме понадобится теперь размещать заказ за 5 дней до исчерпания ее запасов, т.е. при объеме в последние 100 ед.

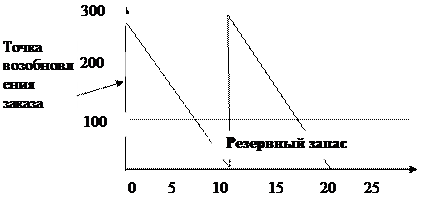
Таким образом, порог возобновления заказа - 100 ед. Когда через 5 дней будет получен новый заказ, фирма как раз использует последние из имевшихся у нее запасов. Этот пример порога возобновления заказа проиллюстрирован на рис. 3.8.

		Время выполнения заказа

Рис. 3.8. Пример порога возобновления заказа

Когда мы допускаем неопределенность в спросе на товарно-материальные запасы, а также в сроках выполнения заказа, становится желательным создание резервного запаса. Эта концепция представлена на рис. 3.9. Верхняя часть рисунка показывает, что произошло бы при наличии у фирмы резервного запаса, равного 100 ед., и при ожидаемом объеме спроса — 200 ед. за каждые 10 дней, а также сроке выполнения заказа 5 дней. Заметим, что если бы резервный запас равнялся 100 ед., порог возобновления заказа следовало бы установить на уровне 200 ед., в отличие от первоначальных 100 ед. Другими словами, порог возобновления заказа определяет объем резервного запаса.

Фактический опыт фирмы из нашего примера показывает рис. 3.10. Из первого сегмента графика спроса видно, что фактический расход оказался несколько меньшим, чем ожидалось. (Наклон линии реального спроса меньше, чем линии ожидаемого, изображенной в верхней части рисунка.) При достижении порога возобновления заказа, равного 200 ед., размещается заказ на дополнительные 200 ед. запасов. Как мы видим, для того, чтобы восполнить запасы, потребовалось 4 дня вместо ожидаемых 5. Во втором сегменте графика расход намного больше, чем ожидалось, в результате чего запасы быстро сокращаются. При остатке запасов 200 ед. снова размещается заказ на 200 ед., но теперь для их получения требуется 6 дней. Под воздействием этих двух факторов происходит серьезное вторжение в резервный запас.

В третьем сегменте графика спроса расход приблизительно равен ожидаемому, т. е. наклон линий ожидаемого и фактического расхода примерно одинаков. Так как в конце предыдущего сегмента расходов запасы были слишком малы, заказ размещается почти немедленно. Срок выполнения заказа оказывается равным 5 дням. В последнем сегменте графика спроса расход немного превышает ожидаемый уровень. Срок, необходимый для получения заказа, составляет 7 дней, что намного больше ожидаемого. Совокупность этих двух факторов снова вынуждает фирму обратиться к резервному запасу. Этот пример демонстрирует важность резервных запасов для компенсации случайных колебаний расхода товарно-материальных ценностей и сроков выполнения заказа. Если бы не было такого запаса, в двух из рассмотренных случаев фирма осталась бы без материалов.

Рис. 3.9. Ожидаемый спрос и время выполнения заказа

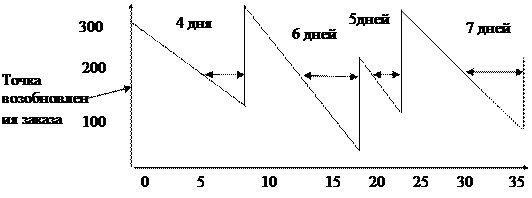
Рис. 3.10 Фактический спрос и время выполнения заказа

ОСНОВНЫЕ ПРОБЛЕМЫ ФОРМИРОВАНИЯ РЕЗЕРВНОГО ЗАПАСА

─ Каков должен быть оптимальный уровень резервного запаса для защиты от дефицита или как часто мы можем допускать дефицит?

─ Каков должен быть уровень возобновления заказа для достижения оптимальной защиты от дефицита?

Модель планирования дефицита

Во многих случаях при закупке товаров у поставщиков экономически выгоднее бывает допустить отсутствие товаров в течение какого-либо промежутка времени, чем поддерживать их постоянное наличие. Для управления запасами в таких системах используется модель, в которой в течение определенного времени запас отсутствует. При этом возможны два варианта:

1. В рамках первого подхода дефицит товаров восполняется по заказам покупателей из следующей поставки. В этом случае максимальная величина запасов равна разнице объема заказа и максимального неудовлетворенного спроса, возникающего в течение времени дефицита (Q – d₁), где d₁ – максимальный размер дефицита.

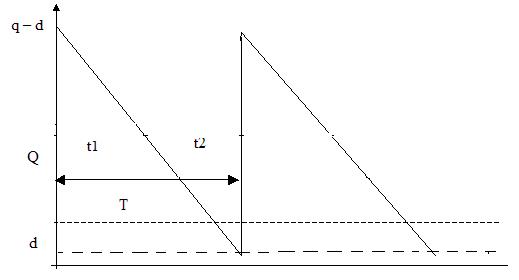
Рис. 3.11. Уровень запасов от времени

Цикл запаса Т (рис. 3.11) состоит из времени потребления запасов t₁ и отсутствия запасов t₂. Таким образом, в течение цикла запаса Т на складе хранится следующее количество запасов:

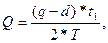(19)

где q – оптимальный размер заказа; d – максимальный размер дефицита.

Аналогично определяется средний уровень дефицита d₁ в течение времени t₂ по формуле:

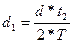. (20)

В условиях известного и линейного спроса D за период (год) количество заказанных партий товара будет составлять D/q, а интервал заказа будет определяться следующей формулой:

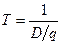. (21)

Таким образом, можно определить t₁ и t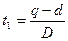₂.

(22)

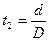(23) (24)

Определяем вид уравнения общей стоимости, включающий три составные части:

1) сумму затрат на подачу заказа = число заказов в год * стоимость подачи одного заказа

С_о∑ = (D/q)* С_о1; (25)

2) сумму затрат по хранению = средний уровень запасов * стоимость хранения единицы запасов за год

C_h∑ = ((q – d)² / 2q* C_h1; (26)

3) сумму издержек отсутствия запасов = средний уровень дефицита * стоимость отсутствия единицы запасов за год

С_d∑ = (d²/2q)* С_d1. (27)

Суммарные затраты на заказ будут определяться следующей формулой:

.

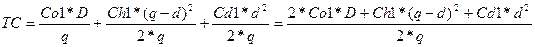Для минимизации данной функции уравнение необходимо продифференцировать по двум независимым переменным q и d. Оптимальный заказ будет равен:

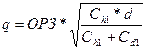, (28)

а максимальный размер дефицита составит:

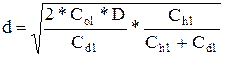. (29)

2. В рамках второго подхода спрос, возникающий на товары в течение времени дефицита, не удовлетворяется. Поэтому максимальный уровень запасов совпадает с объемом заказа. Расчеты общей стоимости запасов будут аналогичны приведенным выше, с учетом замены (q – d) на q и q на (q + d).

В этом случае уравнение общей стоимости примет вид:

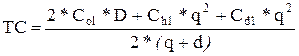. (30)

Применяя операцию дифференцирования по частям, получаем оптимальный размер заказа:

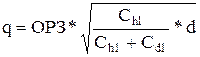, (31)

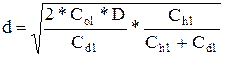. (32)