Машин и аппаратов
Изыскание наиболее рационального метода достижения требуемой точности изделия или его составных частей, изучение взаимосвязи его сборочных единиц, разработка последовательности их комплектации – таковы основные задачи размерного анализа, базирующегося на теории и практике решения размерных цепей.
Размерной цепью называют совокупность взаимосвязанных размеров, образующих замкнутый контур и определяющих взаимное положение поверхностей (или осей поверхностей) одной или нескольких деталей. Замкнутость размерной цепи приводит к тому, что размеры, входящие в размерную цепь, не могут назначаться независимо, т.е. значение и точность, по крайней мере, одного из размеров определяются остальными.
Каждый из размеров, образующих размерную цепь, называют звеном. Любая размерная цепь имеет одно замыкающее звено и одно или несколько составляющих. Замыкающим звеном размерной цепи называют звено исходное при постановке задачи расчета размерной цепи или полученное в результате ее решения.
Составляющими называются все остальные звенья, с изменением которых изменяется и замыкающее звено. В качестве составляющих звеньев размерной цепи могут быть приняты: расстояния между поверхностями или их осями деталей, образующих замыкающее звено; расстояния между поверхностями вспомогательных и основных баз деталей.
Составляющие звенья могут быть увеличивающими или уменьшающими. Увеличивающим называют звено, при увеличении которого (при прочих постоянных) замыкающее звено увеличивается, а уменьшающим – звено, при увеличении которого замыкающее звено уменьшается.
Звенья размерных цепей обозначают буквами латинского алфавита. Для упрощения решения размерных цепей, особенно многозвенных, последние изображают в виде размерных схем. На схеме звенья изображают в виде векторов. Замыкающее звено часто обозначают в квадратных скобках, а его вектор направляют, например, влево. Все векторы уменьшающих звеньев будут направлены, как и замыкающее звено, а векторы увеличивающих звеньев в противоположную сторону.
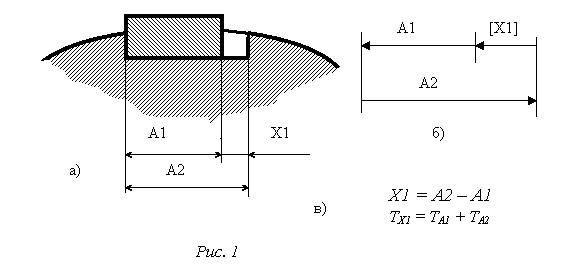
На рис.1а представлено сечение элементарной сборочной единицы: шпонка шириной А1 установлена в шпоночный паз шириной А2. Между шпонкой и стенкой паза зазор X1. Если зазор увеличить, то шпонка, особенно при переменной нагрузке, будет изменять своё положение в пазу, деформироваться, деформировать сопрягаемые поверхности и соединение быстро выйдет из строя. Если зазор уменьшить, то появятся проблемы с монтажом шпонки. Следовательно, есть зазор, который удовлетворит эксплуатацию и производство. Зная номинальный размер зазора и его допуски, можно определить размеры и точность шпонки и паза. Значит Х1 – замыкающее звено, а А1 и А2 составляющие.
Схема такой сборочной размерной цепи представлена на рис.1б. Можно установить, что А1 – уменьшающее звено, а А2 – увеличивающее. Размерная цепь описывается двумя уравнениями (рис. 1в): в номиналах и в допусках. Уравнение в номиналах: замыкающее звено равно сумме увеличивающих звеньев минус сумма уменьшающих. Уравнение в допусках: допуск замыкающего звена равен сумме допусков всех составляющих.
При размерном анализе обычно решаются две задачи: прямая и обратная.
При решении прямой задачи по заданному номинальному размеру и допуску исходного (замыкающего) звена определяют номинальные размеры, допуски и предельные отклонения всех составляющих звеньев размерной цепи.
При решении обратной задачи по установленным номинальным размерам, допускам и предельным отклонениям составляющих звеньев, определяют номинальный размер, допуск и предельные отклонения замыкающего звена.
Решение той или иной задачи расчета размерных цепей при разработке технологического процесса сборки выполняется с целью определения базовых размеров на деталях, выявления не указанных на чертежах зазоров в многозвенных цепях, проверки возможности сборки и отсутствия задеваний вращающихся и неподвижных элементов, снижения точности задания размеров составных частей, определения размеров компенсирующего звена и пр..
В курсовой работе размерный анализ преследует следующие цели: если отсутствуют чертежи составных частей машины, определить базовые размеры составных частей, их допуски и предельные отклонения, проставить полученные значения на эскизах составных частей и убедиться, что установленные значения размеров удовлетворяют требованиям, предъявляемым к замыкающим звеньям; если есть рабочие чертежи составных частей машины, проверить обеспечивают ли размеры, указанные на чертежах, технические требования, предъявленные к замыкающим звеньям, и есть ли возможность уменьшить точность обработки этих размеров.
Рекомендуется следующий порядок размерного анализа конструкций электрических машин и аппаратов.
3.1.Выявление замыкающих звеньев. Для выявления замыкающих звеньев и составления размерных цепей вычерчивается масштабный конструктивный эскиз машины или аппарата (Приложения 14, 16), на котором изображаются только контуры деталей и узлов. На эскиз наносятся осевые размеры замыкающих и составляющих звеньев машины, необходимые для расчета. При этом все размеры, относящиеся к деталям и сборочным единицам, которые не вращаются, даются в верхней части от осевой линии, а размеры вращающихся элементов – в нижней части. Соблюдение этого правила упрощает анализ.
В качестве замыкающих звеньев в электрической машине могут быть гарантированный зазор между торцом подшипника и упором в подшипниковом щите или крышке подшипника, обеспечивающий возможность сборки машины и её надёжность при удлинении ротора в результате нагрева; зазор между крайними точками с торцов якоря или ротора и ближайшими к ним элементами подшипниковых узлов; зазор между элементами вентилятора (если таковой есть) и ближайшими к нему элементами подшипникового щита, диффузора или кожуха; зазор между лобовой частью обмотки статора или полюсной катушки и конструктивными элементами подшипникового щита, исключающий электрический пробой на корпусные детали; величина сдвига поперечных плоскостей, проходящих через середины сердечников ротора (якоря) и статора (полюса), наличие которого приводит к появлению дополнительных осевых сил, действующих на подшипники; величина сдвига щеток от номинального положения их вдоль оси машины на коллекторе или контактных кольцах; установочно-присоединительные и габаритные размеры (размеры заказчика), определяющие положение выходного конца вала относительно отверстий в лапах или опорной поверхности крепительного фланца и т.д.
Особенностью конструкций электрических аппаратов является то, что они, в основном, более простые с точки зрения механики, нет таких жестких требований к функциональным и установочным поверхностям как у электрических машин. А целый класс статических устройств, таких как электронные аппараты, дроссели, резисторы и пр. не имеет специальных требований к механической обработке. Производство электрических аппаратов, как правило, является массовым либо крупносерийным. Для такой организации производства характерно осуществление принципа полной взаимозаменяемости деталей и узлов устройства.
В общем случае анализ размерных цепей электрических аппаратов (также как и электрических машин) проводится с целью решить проектную задачу [16]: по заданным параметрам замыкающего звена определяются параметры составляющих звеньев. Практически при этом по известным предельным отклонениям и допуску замыкающего звена, называемом в этом случае исходным, рассчитываются допуски и предельные отклонения размеров составляющих звеньев.
В качестве замыкающих звеньев электрических аппаратов могут быть воздушные зазоры между якорем и сердечником, регламентированные расстояния между обмоткой и корпусом, воздушный зазор между высоковольтными силовыми контактами и т.д. (Приложения 9, 13, 16, 17). Затем строятся схемы размерных цепей по методике, указанной выше. Таким образом, выявленные исходные (замыкающие) звенья, схемы размерных связей позволяют:
а) правильно разобраться во взаимосвязях деталей, составляющих аппарат и его сборочные единицы;
б) вскрыть заложенные в конструкции методы достижения требуемой точности с помощью каждой из размерных цепей;
в) проанализировать правильность простановки размеров и допусков на чертежах деталей аппарата, внести, если надо, в чертежи поправки;
г) правильно наметить последовательность сборки аппарата и его сборочных единиц.
Пример 9. Выявить замыкающие звенья в конструкции асинхронного двигателя (Приложение 3).
Для выявления замыкающих звеньев и выполнения размерного анализа асинхронного двигателя необходимо составить схему конструкции, выделяя размеры малой величины, чтобы можно было разобраться и обозначить (Приложение 14). Обозначим замыкающие звенья.
Х1 – зазор между выточкой в подшипниковом щите и пружинным кольцом, отжимающим ротор к противоположному подшипниковому щиту, обеспечивающий возможность сборки двигателя и температурную компенсацию при эксплуатации. Если величину этого зазора уменьшить, то за счет определённого сочетания допусков составляющих звеньев подшипники будут зажаты при монтаже подшипниковых щитов и быстро выйдут из строя. Подшипники могут быть зажаты и при эксплуатации за счёт разных температурных расширений, если ротор с валом будут нагреваться больше, чем статор со станиной.
Х2 – расстояние между уступом на валу, в который будет упираться муфта при монтаже на объекте, и осью ближайшего монтажного отверстия в лапе станины (размер заказчика). Обеспечить обязательно, иначе придёт рекламация. Кстати, размеры 80 и 140 тоже размеры заказчика, но они не зависят от сборки, а выполнены при изготовлении вала и станины. И, если эти размеры не соответствуют требования, то вал и станина не должны попасть на сборку.
Х3 – в данном случае это величина, на которую в идеальном случае сердечник ротора длиннее сердечника статора с каждой из сторон. Практически сердечники, как правило, сдвинуты друг относительно друг. В результате сдвига искажается магнитное поле в воздушном зазоре и появляется сила направленная вдоль оси вала, которая нагружает дополнительно подшипники и уменьшает их срок службы. Следовательно, задавая значение Х3, мы ограничим величину смещения сердечников.
Х4 – зазор между вентилятором и кожухом, исключающий вероятность задевания вентилятора за кожух.
Х5 – минимальный зазор между лобовой частью обмотки статора и подшипниковым щитом, исключающий пробой обмотки на корпус при возникновении волновых перенапряжений в сети и в обмотке.
Х6 – габаритный размер (размер заказчика), результат сборки.
Х7 – расстояние между уступом на валу, в который будет упираться муфта при монтаже на объекте, и подшипниковым щитом. Если это размер не выдержан, то муфта будет упираться в щит и тормозить ротор.
Х8 – минимальное расстояние от вентилятора до подшипникового щита.
Х9, Х10 – расстояния от вентиляционных лопаток на роторе до подшипника и ступицы подшипникового щита. В основном определяют эффективность перемещения воздуха, охлаждающего лобовые части обмотки статора.
3.2.Построение схем размерных цепей. Построение схем размерных цепей начинают от одной из поверхностей (осей), ограничивающих замыкающее звено, устанавливая составляющие звенья размерной цепи, участвующие в решении поставленной задачи, и доходят до второй поверхности (оси), ограничивающей замыкающее звено.
При составлении схемы размерной цепи величины составляющих звеньев необходимо брать из чертежей (если таковые есть) деталей и сборочных единиц, входящих в состав машины или аппарата. Если чертежей составных частей нет, то необходимо набросать эскизы составных частей и проставить на них размеры, как на чертежах (учесть опыт, полученный на производственных практиках и при выполнении курсовых проектов по дисциплинам «Электрические машины», «Проектирование электрических машин», «Электрические и электронные аппараты», «Основы теории электрических аппаратов» и использовать их для составления размерных цепей. Номинальные значения составляющих звеньев замерить на сборочном чертеже, учитывая масштаб изображения.
Пример 10.Составить для асинхронного двигателя (Приложение 3) с учётом схемы конструкции для размерного анализа (Приложение 14) размерные цепи для замыкающих звеньев Х1, Х2, Х3.
Построение размерной цепи для замыкающего звена Х1 (см. Приложения 14 и 15А). Направляем вектор Х1 влево (можно в любую сторону). Слева зазор Х1 ограничен торцовой поверхностью отверстия под подшипник в ступице подшипникового щита, а справа стороной пружинного кольца. Пружинное кольцо толщиной А1 в свою очередь упирается в наружную обойму подшипника. Если размер А1 зафиксировать в зоне контакта с обоймой подшипника и увеличивать в сторону зазора, то зазор Х1 (замыкающее звено) будет уменьшаться. Следовательно, размер А1 уменьшающее составляющее звено, его вектор имеет то же направление, что и замыкающее звено и примыкает к замыкающему звену справа.
Как отмечено выше, справа к пружинному кольцу примыкает неподвижная (наружная) обойма шарикоподшипника. В шарикоподшипниках очень мал рабочий зазор между телами качения. Считается, что торцовые плоскости наружной и внутренней обойм совпадают. Можно полагать, что справа к пружинному кольцу примыкает подвижная (внутренняя) обойма шарикоподшипника с осевым размером А2, которая в свою очередь упирается в ступень вала с размером А3. Таким образом осуществлён переход от неподвижных элементов машины к вращающемся.
Если размер А2 зафиксировать справа и увеличивать его влево, то он будет влево перемещать размер А1, который упираясь в замыкающее звено Х1 будет его уменьшать. Следовательно, звено А2 тоже уменьшающее, имеет направление замыкающего звена и справа примыкает к звену А1.
Так же можно показать, что размеры А3 и А4 уменьшающие со всеми отсюда вытекающими последствиями. А4 – осевой размер шарикоподшипника, внутренняя обойма которого прилегает к торцу ступени А3. Как и ранее, можно перейти от внутренней (вращающейся) ступени к наружной (неподвижной), прилегающей справа к торцовой поверхности отверстия под подшипник в ступице подшипникового щита.
Размер А5 определяет положение торца отверстия в ступице подшипникового щита относительно торца замка подшипникового щита и прилегает справа к А4, а слева к замковой поверхности станины. Если размер А5 зафиксировать слева и увеличивать вправо, то он потянет за собой неизменные размеры А4, А3, А2, А1 и Х1 будет увеличиваться. Следовательно, А5 увеличивающий размер и будет иметь направление противоположное направлению замыкающего звена.
К размеру А5 слева примыкает размер А6 (расстояние между замками станины), а к последнему – размер А7 (расстояние от замка подшипникового щита до торца отверстия под подшипник в ступице). Размер А7 примыкает к левой стороне замыкающего звена Х1, тем самым замыкая размерную цепь.
Построение размерной цепи для замыкающего звена Х2 (Приложение 15Б) выполняется, как для Х1. Вектор Х2 направим влево. Слева к Х2 прилегает размер В1 (расстояние от упора на валу, в который будет упираться муфта, до упора, в который упирается подшипник). Этот размер обычно есть на чертеже вала или ротора. Если В1 зафиксировать справа и увеличивать влево, то замыкающее звено Х2 будет увеличиваться. Следовательно В1 по отношению к Х2 увеличивающее звено и будет направлено встречно направлению Х2. По той же причине А3 и А4 в данной цепи увеличивающие звенья, а звенья А5 и А6 – уменьшающие. Размер В2 (расстояние от торца замковой поверхности станины до оси отверстия в лапе станины – обычно указан на чертеже станины или статора) – увеличивающее звено, примыкающее к правой стороне Х2 и замыкающее размерную цепь.
 Построение размерной цепи для замыкающего звена Х3 (Приложение 15В). Замыкающее звено Х3 ограничено слева торцом сердечника ротора, напрессованным на вал, а справа торцом сердечника статора, запрессованным в станину. Слева к замыкающему звену Х3 примыкает размер С1, проставленный на чертеже ротора и определяющий положение сердечника ротора на валу. Звено С1 уменьшающее и направлено согласно с замыкающим звеном. За С1 следуют увеличивающие составляющие звенья А3 и А4, уменьшающие А5 и А6 и увеличивающее С2, которое замыкает размерную цепь примыкая справа к замыкающему звену. С2 – размер, определяющий положение сердечника статора от торца замковой поверхности после запрессовки в станину.
Построение размерной цепи для замыкающего звена Х3 (Приложение 15В). Замыкающее звено Х3 ограничено слева торцом сердечника ротора, напрессованным на вал, а справа торцом сердечника статора, запрессованным в станину. Слева к замыкающему звену Х3 примыкает размер С1, проставленный на чертеже ротора и определяющий положение сердечника ротора на валу. Звено С1 уменьшающее и направлено согласно с замыкающим звеном. За С1 следуют увеличивающие составляющие звенья А3 и А4, уменьшающие А5 и А6 и увеличивающее С2, которое замыкает размерную цепь примыкая справа к замыкающему звену. С2 – размер, определяющий положение сердечника статора от торца замковой поверхности после запрессовки в станину.
Замечание. В практике возможен случай, когда сердечники статора и ротора равны. Тогда номинальное значение замыкающего звена равно нулю и не ясно, как задать ему направление. Можно применить искусственный приём: стороны, ограничивающие замыкающее звено разнести, как показано на рис 2. Теперь ясно видно, что левую сторону замыкающего звена ограничивает торец сердечника ротора, а правую – торец сердечника статора и можно задать направление вектора замыкающего звена при построении схемы размерной цепи.
3.3.Составление основных уравнений размерных цепей. Уравнения размерных цепей упоминали выше и привели пример для элементарной размерной цепи на рис. 1. Для общего случая уравнения размерных цепей имеют вид:
уравнение в номиналах
 , (1)
, (1)
где: X– замыкающее звено размерной цепи;
Aувi – увеличивающие звенья размерной цепи;
Aумk – уменьшающие звенья размерной цепи;
m – число увеличивающих звеньев;
n– число уменьшающих звеньев;
уравнение в допусках
 (2)
(2)
где: TX – допуск замыкающего звена;
TAj – допуски составляющих звеньев.
Уравнения 1 и 2 являются основой для размерного анализа конструкции изделия.
Пример 11.Записать уравнения для размерных цепей с замыкающими звеньями Х, Х2, Х3, представленных в Приложении 15.
Для замыкающего звена Х1
Х1=(А5+А6+А7)–(А1+А2+А3+А4),
ТХ1=ТА1+ ТА2+ ТА3+ ТА4+ ТА5+ ТА6+ ТА7.
Для замыкающего звена Х2
Х2=(В1+В2+А3+А4)–(А5+А6),
ТХ2=ТВ1+ ТВ2+ ТА3+ ТА4+ ТА5+ ТА6 .
Для замыкающего звена Х3
Х3=(С2+А3+А4)–(С1+А5+А6),
ТХ3=ТС1+ ТС2+ ТА3+ ТА4+ ТА5+ ТА6.
3.4.Расчёт размерных цепей. В зависимости от поставленной задачи и производственных условий технологические размерные цепи рассчитываются следующими методами: на максимум и минимум (метод полной взаимозаменяемости); вероятностным методом (метод ограниченной взаимозаменяемости); методом групповой взаимозаменяемости (при селективной сборке); метод регулирования; метод пригонки.
При выборе метода достижения точности замыкающего звена необходимо учитывать функциональное назначение изделий по конструктивным и технологическим особенностям, стоимость изготовления и сборки, тип производства и другие факторы.
Заданная точность замыкающего звена должна достигаться с наименьшими технологическими и производственными затратами. При прочих равных условиях рекомендуется выбирать в первую очередь такие методы достижения точности, при которых сборка производится без подбора, пригонки и регулирования, т.е. методы полной и ограниченной взаимозаменяемости.
Сущность метода полной взаимозаменяемости состоит в том, что точность замыкающего звена обеспечивается у всех без исключения изделий, без какого-либо подбора звеньев или их пригонки. При этом допуски составляющих звеньев рассчитываются по методу максимума – минимума, при котором учитываются только предельные отклонения составляющих звеньев.
Преимущества метода полной взаимозаменяемости: использование его при сборке превращает её в простое соединение деталей; простота нормирования процесса сборки; возможность автоматизации сборочных процессов (отсутствуют операции пригонки); возможность кооперирования и специализации участков, цехов, предприятий.
При размерном анализе конструкции машины или аппарата в курсовой работе необходимо решить прямую задачу, установив допуски и предельные отклонения всех составляющих звеньев по параметрам замыкающего звена. Прямая задача может быть решена двумя способами: способ пробных расчётов и способ с использованием регулировочного звена.
Способ пробных расчётов включает этапы: назначение допусков на составляющие звенья; определение допуска замыкающего звена (обратная задача); сравнение расчётного допуска замыкающего звена с исходным; если значения не совпадают с определённой точностью, корректировка допусков составляющих звеньев; повторный расчёт допуска замыкающего звена и так до получения определённого совпадения заданного и расчётного значений.
Способ расчётов с регулирующим звеном отличается тем, что корректируются допуски не всех составляющих звеньев, а одного, которое и называется регулирующим. В качестве регулирующего звена может быть принято любое составляющее звено размерной цепи, но удобно принимать звено, точная обработка и измерение которого не вызывает затруднений, а размер относительно велик.
Допуски на составляющие звенья можно назначить следующим образом.
Если есть представление о точности составляющего звена и методе обработки его поверхностей, то допуски назначают, исходя из средней экономической точности [7, табл. 2.66], [38, с. 8–15, табл. 4, 5]. В противном случае можно исходить из среднего размера и среднего допуска.
Средний размер составляющего звена при расчёте методом полной взаимозаменяемости определить по формуле
 , (3)
, (3)
где Ai – составляющие звенья размерной цепи;
q – число составляющих звеньев, для которых допуски известны. Это могут быть стандартные изделия (например, подшипники), для которых допуски можно найти в справочниках, или унифицированные, для которых допуск можно взять из чертежа.
Средний допуск для среднего составляющего звена можно определить по формуле
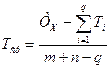 (4)
(4)
где ТХ – указанный в задании допуск замыкающего звена;
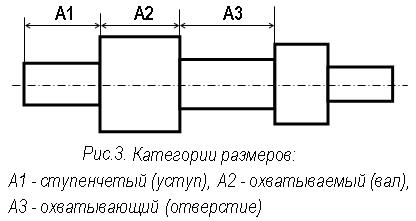 Ti – известные допуски составляющих звеньев размерной цепи, число которых равно q.
Ti – известные допуски составляющих звеньев размерной цепи, число которых равно q.
По Аср и Тср из [7, табл. 1.8] определить квалитет. По установленному квалитету из [7, табл. 1.8] определить допуски на размеры составляющих звеньев.
Устанавливая допуски на размеры составляющих звеньев, одновременно необходимо определить предельные отклонения в зависимости от категории размера (рис.3). Для охватывающих размеров допуск ставится в плюс, например Ø 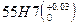 , для охватываемых – в минус Ø
, для охватываемых – в минус Ø 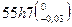 , для ступенчатых – ± половина допуска Ø
, для ступенчатых – ± половина допуска Ø 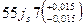 .
.
По установленным на составляющие звенья допускам, рассчитать допуск замыкающего звена по формуле
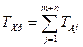 (5)
(5)
где: TXр – расчётное значение допуска замыкающего звена;
TAj – допуски составляющих звеньев.
Полученное расчётное значение допуска замыкающего звена ТXр сравнить с заданным значением ТX. Если ТXр не равно ТX , необходимо сменить допуски составляющих звеньев либо регулирующего звена (в зависимости от принятого способа решения задачи) и повторить расчеты, пока ТXр не станет равным ТX . Следует отметить, что, в порядке исключения, допуск на размер одного из составляющих звеньев может быть установлен не стандартный.
После установления величин допусков составляющих звеньев, необходимо уточнить их предельные отклонения. Для этого необходимо составить и решить уравнение размерной цепи в средних отклонениях. Среднее отклонение размера определяется выражением
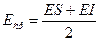 (6)
(6)
где: Eср – среднее отклонение размера;
ES – верхнее предельное отклонение размера;
EI – нижнее предельное отклонение размера.
Уравнение в средних отклонениях имеет вид
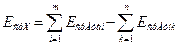 , (7)
, (7)
Решив это уравнение, получим расчётное значение среднего отклонения замыкающего звена EсрXр, а через него верхнее предельное расчётное отклонение размера замыкающего звена
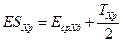 (8)
(8)
и его нижнее предельное расчётное отклонение
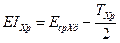 . (9)
. (9)
Если полученные значения предельных отклонений ESXp и EIXp равны заданным предельным отклонениям допуска ТX то расчёт закончен. Если предельные отклонения ESХp и EIХp отличаются от заданных значений, то для размеров всех составляющих звеньев или регулировочного звена не меняя допусков изменить предельные отклонения, выбирая стандартные из [7, табл. 1.9 – 1.12], и повторить расчёты, показначения ESXp и EIXp не станут равны исходным данным. Следует отметить, что, в порядке исключения, предельные отклонения на размер одного из составляющих звеньев могут быть установлены не стандартные.
Пример 12.Решить размерную цепь (Приложение 15В) методом полной взаимозаменяемости, определив допуски и основные предельные отклонения для составляющих звеньев. Исходные данные в Приложении 1.
Исходные данные: параметры замыкающего звена Х3=1±1 мм, ESX3=1 мм, EIX3= –1 мм, TX3= ESX3– EIX3 =1 – (–1)=2 мм.
Основные уравнения размерной цепи (см. пример 11)
Х3=(С2+А3+А4)–(С1+А5+А6),
ТХ3=ТС1+ ТС2+ ТА3+ ТА4+ ТА5+ ТА6.
Дополнительные данные: осевая длина подшипников (Приложение 14) А4=21 мм (размер подшипника 180307 (см. спецификацию, Приложение 2) из справочника по подшипникам), допуск ТА4=0,12 мм, основные отклонения: ESA4 =0, EIA4 = – 0,12 мм [8, табл. 4.82]; номинальные размеры остальных составляющих звеньев из сборочного чертежа с учётом масштаба изображения: С1 = 48 мм, С2 = 53 мм, А3 = 200 мм, А5 = 19 мм, А6 = 206 мм.
Решать размерную цепь будем способом с использованием регулировочного звена. В качестве регулировочного выбираем наибольшее составляющее звено А6 = 206 мм.
Подставим полученные размеры в уравнение в номиналах и проверим правильность измерений
Х3 = (53+200+21)–(48+19+206) = 1.
Номинальное значение замыкающего звена обеспечивается.
Определим средний размер составляющего звена по формуле (3) с учётом, что m=3, n=3, q=1
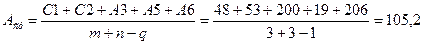 мм.
мм.
Определим средний допуск для среднего составляющего звена по формуле (4)
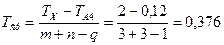 мм.
мм.
Из [7, табл. 1.8] следует, что точность размера Аср=105,2 мм при допуске Тср=0,376 мм соответствует 12 квалитету. По 12 квалитету назначим допуски из [7, табл. 1.8] для всех составляющих звеньев, кроме А4, и для удобства занесём всю информацию по составляющим звеньям в табл. 1.
Таблица 1
| Составляющее звено | Номинальный размер (мм) | Вид звена | Категория размера | Допуск предварительно (мм) | Допуск откорректированный (мм) |
| С1 | уменьшающее | уступ | 0,25 | 0,25 | |
| С2 | увеличивающее | уступ | 0,3 | 0,3 | |
| А3 | увеличивающее | вал | 0,46 | 0,46 | |
| А4 | увеличивающее | вал | 0,12 | 0,12 | |
| А5 | уменьшающее | уступ | 0,21 | 0,21 | |
| А6 | уменьшающее | вал | 0,46 | 0,66 |
По формуле (2) определим расчётное значение допуска замыкающего звена в зависимости от назначенных допусков составляющих звеньев
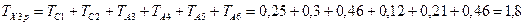 мм
мм
Расчетный допуск замыкающего звена меньше исходного. Поэтому меняем допуск регулировочного составляющее звено А6 = 206 мм в сторону увеличения. Но подходящего стандартного значения допуска в [7, табл. 1.8] нет. Поэтому устанавливаем для A6 не стандартный допуск ТА6 = 0,66 мм, что для одного звена допускается, и повторяем расчёт.
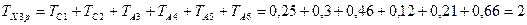 мм
мм
Полученное значение расчётного допуска замыкающего звена равно исходному значению. Запишем размеры составляющих звеньев с установленными допусками, учитывая категорию размеров (см. рис. 3): С1=48±0,125, С2=53±0,15, А3=200–0,46, А4=21–0,12, А5=19±0,105, А6=206–0,66.
Необходимо проверить обеспечат ли установленные предельные отклонения составляющих звеньев заданные предельные отклонения замыкающего звена.
Для этого по формуле (6) определим средние отклонения размеров составляющих звеньев: EсрС1 = 0, EсрС2 = 0, EсрА3 = – 0,23, EсрА4 = – 0,06, EсрА5 = 0, EсрА6 = – 0,33.
Запишем для размерной цепи уравнение в средних отклонениях по форме (7) и, решив его, определим расчетное значение среднего отклонения размера замыкающего звена EсрХр.

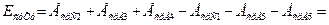
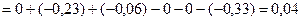
По формулам (8) и (9) определим расчётные верхнее и нижнее предельные отклонения размера замыкающего звена:
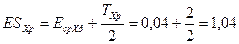 ;
; 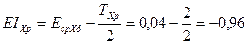 .
.
Расчётные значения предельных отклонений размера замыкающего звена не соответствуют исходным данным. Поэтому необходимо откорректировать предельные отклонения размера в данном случае регулировочного звена. Пусть 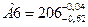 , тогда
, тогда 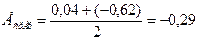 и
и
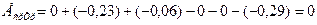 .
.
Для регулировочного звена установлены не стандартные значения предельных отклонений (в справочнике нет приемлемых значений), но это допускается для одного из составляющих звеньев.
В этом случае расчётные верхнее и нижнее предельные отклонения размера замыкающего звена удовлетворяют заданию:
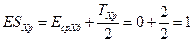 ;
; 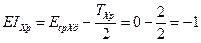 .
.
Пример 13. Решить размерную цепь (Приложение 16а) втягивающего реле постоянного тока стартера автомобиля определив допуски и основные предельные отклонения для составляющих звеньев.
Замыкающим (исходным) звеном данного устройства является воздушный зазор Х1 между якорем и магнитопроводом (стопом). Величина зазора влияет на величину тягового усилия и быстродействие втягивающего реле. При проектировании было заложено, что величина воздушного зазора равна Х1 = 10 ± 0,3 мм.
Построим схему размерной цепи для замыкающего звена Х1 (Приложение 16б). По линии якоря размеры А2, А3 и А4 – уменьшающие звенья, А1 –увеличивающее звено. Все звенья относятся к конкретной детали и имеют размеры на соответствующих чертежах.
Номинальные размеры составляющих звеньев из сборочного чертежа с учетом масштаба изображения: стоп А2 = 40 мм; длина якоря до пружинной шайбы А3 = 78 мм, толщина пружинной шайбы А4 = 2 мм; длина стакана (корпуса) А1 = 130 мм.
Уравнение размерной цепи для замыкающего звена будет выглядеть следующим образом:
Х1 = А1 – (А2 + А3 + А4).
Подставим полученные размеры в уравнение в номиналах и проверим правильность измерений
Х1 = 130 – (40 + 78 + 2) = 10 мм .
Номинальное значение замыкающего звена обеспечивается. Расчет допусков составляющих звеньев определим методом полной взаимозаменяемости. Определим средний размер составляющего звена с учётом, что m=1 число увеличивающих звеньев, n=3 число уменьшающих звеньев, q=0 число звеньев, для которых известны допуски, для пружинного кольца можно было бы подобрать стандартное изделие с известным допуском, но в данном случае кольцо оригинальное со своим чертежом.
Определим среднюю величину размера составляющих звеньев:
 мм .
мм .
Определим средний допуск составляющего звена с учётом, что поле допуска замыкающего звена Т1 = 0,3 – (-0,3) = 0,6 мм :
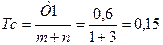 мм.
мм.
По среднему размеру Ас и среднему допуску Тс из [7, табл. 1.8] определим, что точность нестандартных составляющих звеньев соответствует примерно 10, 11 квалитету.
Установим для каждого звена допуск по 11 квалитету и для удобства занесём всю информацию по составляющим звеньям в табл. 2.
Проверим по формуле (5.2) [16] поле допуска замыкающего звена при наличии предварительно принятых допусков:
Таблица 2
| Составляющее звено | Номинальный размер (мм) | Вид звена | Категория размера | Допуск предварительно (мм) | Допуск откорректированный (мм) |
| А1 | увелич. | вал | - 0,25 | - 0,11 -0,3 | |
| А2 | уменьш. | вал | - 0,16 | -0,16 | |
| А3 | уменьш. | вал | - 0,19 | - 0,19 | |
| А4 | уменьш. | вал | - 0,06 | - 0,06 |
Т1´ = ТА1+ТА2+ТА3+ТА4 = 0,25+0,16+0,19+0,06 =0,66 мм .
Полученное поле допуска превышает величину установленного допуска Т1=0,6 мм и заданное условие расчета не выполнено. Это вынуждает выбрать регулирующее звено, размер которого должен быть выполнен точнее 11 квалитета, принятого для всех остальных звеньев. В качестве регулирующего звена избираем размер А1=130 мм, выполнение которого и измерение не вызывает затруднений, а абсолютная величина допуска у этого размера больше, чем у других размеров, и может быть уменьшена, не вызывая дополнительных существенных затрат.
Допуск регулирующего звена А1 определим по формуле (5.11)[16]:
ТА1=Т1 – (ТА2+ТА3+ТА4) = 0,6 –(0,16+0,19+0,06) = 0,19 мм .
Звено А1 является увеличивающим, поэтому координата середины поля допуска определяется для него по формуле (5.12)[16]:
ЕсА1 = ЕсХ1 + (ЕсА2+ЕсА3+ЕсА4) = 0 + (-0,08-0,095-0,03)= -0,205
ЕсХ1=(ЕSX1+EIX1)0,5 = (0,3+(-0,3))0,5 =0
EcA2=(ESA2+EIA2)0,5 = (0+(-0,16))0,5 = -0,08
EcA3=(ESA2+EIA2)0,5 = (0+(-0,19))0,5 = -0,095
EcA4=(ESA4+EIA4)0,5 = (0+(-0,06))0,5 = -0,03
Предельные отклонения регулирующего звена А1 определим по известным формулам:
ESA1 = EcA1+TA1/2 = -0,205+0,19/2 = - 0,11
EIA1= EcA1- TA1/2 = -0,205 - 0,19/2 = -0,3 .
Размер регулирующего звена 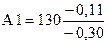
Проверим полученные результаты. Определим максимальное и минимальное значение замыкающего звена, используя полученные допуски увеличивающих и уменьшающих звеньев:
Х1max = A1max – (A2min+A3min+A4min)=129,89 – (39,84+77,81+1,94)=10,3
X1min =A1min – (A2max+A3max+A4max)=129,7 – (40+78+2) = 9,7
Расчет сделан правильно.
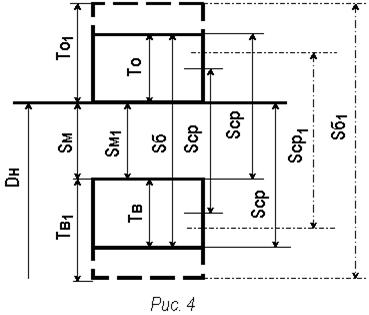 Метод полной взаимозаменяемости экономически целесообразно использовать при малом числе составляющих звеньев размерной цепи (
Метод полной взаимозаменяемости экономически целесообразно использовать при малом числе составляющих звеньев размерной цепи ( 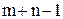 < 4). При увеличении числа составляющих звеньев значительно уменьшаются допуски на их размеры, что может привести к удорожанию изделия за счёт повышения стоимости механической обработки.
< 4). При увеличении числа составляющих звеньев значительно уменьшаются допуски на их размеры, что может привести к удорожанию изделия за счёт повышения стоимости механической обработки.
Сущность метода неполной взаимозаменяемости состоит в том, что точность замыкающего звена обеспечивается не у всех изделий, а только у заранее обусловленной их части. При этом предварительно устанавливается процент риска P, т.е. процент изделий, у которых может не обеспечиваться точность замыкающего звена. Следует отметить, что процент риска – лишь вероятность получения бракованных изделий. Поясним это примером: пусть необходимо выполнить сопряжение вала с отверстием (подшипник скольжения), обеспечив определенную степень точности зазора между ними (рис. 4).
На рис. 4: Dн – номинальный размер сопряжения, Tо и Tв – допуски соответственно отверстия и вала, полученные методом расчета размерных цепей на минимум – максимум. Следовательно, допуски Tо и Tв обеспечат сборку по методу полной взаимозаменяемости, т.е. в большой партии сопряжений зазор между отверстием и валом может колебаться в пределах от минимального Sм до максимального Sб, при которых обеспечивается заданный срок службы сопряжения. Однако, вероятность того, что в сопряжении получится минимальный Sм или максимальный Sб зазоры очень мала, зато средних Sср зазоров или близких к ним будет большинство.
Учитывая, что настройка оборудования для механической обработки чаще всего осуществляется на середину допуска, можно увеличить допуски на сопрягаемые поверхности, например, до Tо1 и Tв1 (рис. 4). В этом случае среднее значение зазора Sср1 по-прежнему будет меньше допустимого Sб, но есть вероятность того, что из годных деталей может быть собрано сопряжение с зазором больше допустимого, т.е. брак. Но такого сочетания деталей в партии может и не получиться, а если и получится, то сопряжение можно разобрать и подобрать из партии детали, обеспечивающие допустимый зазор.
Таким образом, использование метода неполной взаимозаменяемости для обеспечения точности замыкающего звена экономически целесообразно в многозвенных размерных цепях. При этом допуски составляющих звеньев могут быть значительно больше, чем при использовании метода полной взаимозаменяемости. Расчет параметров составляющих звеньев в этом случае производят вероятностным методом, который базируется на законах рассеяния размеров деталей в партии.
В теории размерных цепей наиболее часто применяются следующие основные законы рассеяния размеров деталей: нормальный закон, закон равной вероятности, закон треугольника.
Нормальный закон (закон Гаусса) – наиболее часто встречающийся и применяемый в технических приложениях теоретический закон рассеяния случайных погрешностей. Нормальный закон характеризует рассеяние угловых и линейных размеров деталей при обработке их на настроенных станках (станках – автоматах), если на производстве соблюдаются определенные условия (стабильность работы оборудования и приспособлений, несущественный износ режущего инструмента и др.).
Теоретическая кривая рассеяния размеров по нормальному закону на рис. 5, где Ai – текущее значение размера, y – частота появления определенного размера, Amin и Amax – соответственно минимальное и максимальное допустимые) значения размеров, Ti – допуск на размер, Ā – математическое ожидание, равное среднему арифметическому размеру в партии изделий.
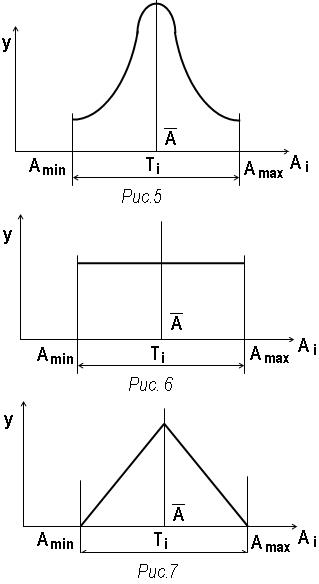 Закон равной вероятности описывает рассеяние размеров, если среди причин, вызывающих производственные погрешности имеется одна, резко доминирующая по силе воздействия и равномерно изменяющаяся во времени (например, влияние равномерного значительного износа режущего инструмента). Частота появления размера является в этом случае величиной постоянной (рис. 6).
Закон равной вероятности описывает рассеяние размеров, если среди причин, вызывающих производственные погрешности имеется одна, резко доминирующая по силе воздействия и равномерно изменяющаяся во времени (например, влияние равномерного значительного износа режущего инструмента). Частота появления размера является в этом случае величиной постоянной (рис. 6).
Закон треугольника может возникать при суммировании двух независимых случайных величин, распределение размеров которых подчиняется закону равной вероятности. Такая зависимость частоты появления размеров представлена на рис. 7.
Для получения основных расчетных зависимостей вероятностного метода расчета размерных цепей используют теоремы о математических ожиданиях и дисперсиях. При изготовлении деталей математическое ожидание (средний арифметический размер) в партии может не совпадать с серединой поля допуска. Величина такого несовпадения, выраженная в долях половины допусков Ti, называется коэффициентом относительной асимметрии ai. Другой величиной, используемой при вероятностном методе расчета, является коэффициент относительного рассеяния li, равный отношению среднеквадратичного отклонения размеров si к половине допуска Ti.
Численные значения ai и li зависят от условий и масштаба производства и различны для разных категорий размеров, технологических операций и методов обработки. При производственных расчетах фактические значения ai и li определяются экспериментально по результатам анализа точности технологических процессов.
При выполнении курсовой работы следует принять 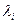 = 0,333 для нормального закона распределения,
= 0,333 для нормального закона распределения, 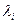 = 0,577 для распределения равной вероятности и
= 0,577 для распределения равной вероятности и 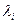 = 0,408 для распределения по треугольнику. Коэффициенты относительной асимметрии могут быть заданы в зависимости от особенностей размеров (рис. 3) составляющих звеньев: для охватывающих (отверстий) αо=+0,25 ÷ –0,25 (чаще отрицательные), для охватываемых (валов) αв=+0,3 ÷ –0,2 (чаще положительные), и для ступенчатых (уступов) αс=+0,2 ÷ –0,2 (обычно близкие к нулю). Риск чаще всего принимается равным P = 0,27%. Практически при таком риске количество сборочных единиц, выходящих за пределы допуска может быть не более трех на 1000 изделий, а может и не быть вообще. Коэффициент, зависящий от процента риска в данном случае равен t = 3. Если необходимо установить другой процент риска Р и коэффициент t их можно выбрать из табл. 3.
= 0,408 для распределения по треугольнику. Коэффициенты относительной асимметрии могут быть заданы в зависимости от особенностей размеров (рис. 3) составляющих звеньев: для охватывающих (отверстий) αо=+0,25 ÷ –0,25 (чаще отрицательные), для охватываемых (валов) αв=+0,3 ÷ –0,2 (чаще положительные), и для ступенчатых (уступов) αс=+0,2 ÷ –0,2 (обычно близкие к нулю). Риск чаще всего принимается равным P = 0,27%. Практически при таком риске количество сборочных единиц, выходящих за пределы допуска может быть не более трех на 1000 изделий, а может и не быть вообще. Коэффициент, зависящий от процента риска в данном случае равен t = 3. Если необходимо установить другой процент риска Р и коэффициент t их можно выбрать из табл. 3.
В курсовой работе виды распределений составляющих звеньев и значение коэффициента относительной асимметрии указываются в задании на работу (см. Приложение 1).
Таблица 3
Значение коэффициента t для различных процентов риска P
| P | 0,01 | 0,05 | 0,1 | 0,27 | 0,5 | ||||||
| t | 3,89 | 3,48 | 3,29 | 2,81 | 2,57 | 2,32 | 2,17 | 1,96 | 1,65 |
Решение прямой задача расчёта размерной цепи вероятностным методом также может быть выполнено двумя способами: способ пробных расчётов и способ с использованием регулировочного звена.
Допуски на составляющие звенья можно назначить исходя из средней экономической точности [7, табл. 2.66], [38, с. 8–15, табл. 4, 5] или, исходя из среднего размера и среднего допуска.
Средний размер составляющего звена определить по формуле (3)
Средний допуск для среднего составляющего звена при расчётах вероятностным методом можно определить по формуле
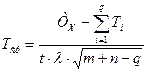 , (10)
, (10)
где ТХ – указанный в задании допуск замыкающего звена;
t – коэффициент, зависящий от процента риска;
λ – коэффициент относительного рассеяния, определяемый заданным распределением;
Ti – известные допуски составляющих звеньев размерной цепи, число которых равно q.
По Аср и Тср из [7, табл. 1.8] определить квалитет. По установленному квалитету из [7, табл. 1.8] определить допуски на размеры составляющих звеньев, установив предельные отклонения в зависимости от категории размера (см. рис. 3).
Определить коэффициент относительной асимметрии αХ для замыкающего звена по формуле
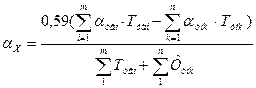 , (11)
, (11)
где αувi – коэффициенты относительной асимметрии увеличивающих звеньев с учётом категории их размеров;
Тувi – допуски увеличивающих звеньев;
αумk – коэффициенты относительной асимметрии уменьшающих звеньев с учётом категории их размеров;
Тумk – допуски уменьшающих звеньев;
Определить коэффициент относительного рассеяния lХ для замыкающего звена по формуле
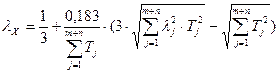 , (12)
, (12)
где lj – коэффициенты относительного рассеяния всех составляющих звеньев;
Тj – допуски всех составляющих звеньев;
По установленным на составляющие звенья допускам, рассчитать допуск замыкающего звена по формуле
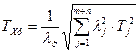 . (13)
. (13)
Полученное расчётное значение допуска замыкающего звена ТХр сравнить с заданным значением ТХ. Расчётное значение ТХр должно быть либо равно заданному ТХ, либо меньше его, но не более чем на 10% для курсовой работы (проекта). Если ТХр не укладывается в указанный диапазон, необходимо сменить допуски составляющих звеньев либо регулирующего звена (в зависимости от принятого способа решения задачи) и повторить расчеты, пока ТХр не войдёт в заданный диапазон. Следует отметить, что, в порядке исключения, допуск на размер одного из составляющих звеньев может быть установлен не стандартный.
После установления величин допусков составляющих звеньев, необходимо уточнить их предельные отклонения. Для этого определить значение среднего отклонения Eсхр расчётного допуска замыкающего звена по формуле
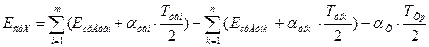 , (14)
, (14)
где 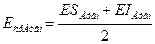 ;
; 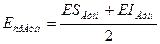 .
.
Верхнее предельное расчётное отклонение размера замыкающего звена
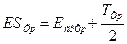 . (15)
. (15)
Нижнее предельное расчётное отклонение размера замыкающего звена
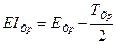 . (16)
. (16)
Если полученные значения предельных отклонений ESХp и EIХp укладываются в диапазон допуска ТХ то расчёт закончен. Если предельные отклонения ESХp и EIХp не укладываются в указанный диапазон, то в размерах составляющих звеньев или регулировочного звена не меняя допусков изменить предельные отклонения и вновь рассчитать ESХp и EIХp. Следует отметить, что, в порядке исключения, предельные отклонения на размер одного из составляющих звеньев могут быть установлены не стандартные.
Пример 14.Решить размерную цепь (Приложение 15В) вероятностным методом (метод ограниченной взаимозаменяемости), определив допуски и основные предельные отклонения для составляющих звеньев. Исходные данные в Приложении 1.
В примере рассмотрим решение вероятностным методом размерной цепи, решённой в примере 12 методом полной взаимозаменяемости.
Исходные данные: параметры замыкающего звена Х3=1 мм, ESX3=1 мм, EIX3= –1 мм, TX3= ESX3– EIX3 =1 – (–1)=2 мм; коэффициенты относительного рассеяния для подшипников 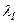 = 0,333, для прочих составляющих звеньев
= 0,333, для прочих составляющих звеньев 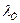 = 0,408; коэффициенты относительной асимметрии aоi = – 0,21, aвi = 0,24, aсi = 0,02.
= 0,408; коэффициенты относительной асимметрии aоi = – 0,21, aвi = 0,24, aсi = 0,02.
Основные уравнения размерной цепи
Х3=(С2+А3+А4)–(С1+А5+А6),
ТХ3=ТС1+ ТС2+ ТА3+ ТА4+ ТА5+ ТА6.
Дополнительные данные см. в примере 12.
Подставим полученные размеры в уравнение в номиналах и проверим правильность измерений
Х3 = (53+200+21)–(48+19+206) = 1.
Номинальное значение замыкающего звена обеспечивается.
Определим средний размер составляющего звена с учётом, что m=3, n=3, q=1
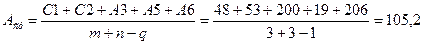 мм
мм
Определим средний допуск составляющего звена с учётом, что риск Р=0,27%, t=3, 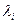 = 0,408
= 0,408
 мм.
мм.
По среднему размеру Аср и среднему допуску Тср из [7, табл. 1.8] определим, что точность нестандартных составляющих звеньев соответствует примерно 13, 14 квалитету, установим для каждого звена допуск по 14 квалитету и для удобства занесём всю информацию по составляющим звеньям в табл. 4.
По формуле 12 определим коэффициент относительного рассеяния lХ3 для замыкающего звена
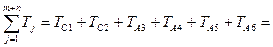
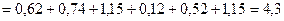

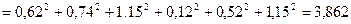
Таблица 4
| Составляющее звено | Номинальный размер (мм) | Вид звена | Категория размера | ai | Допуск предварительно (мм) | Допуск откорректированный (мм) |
| С1 | уменьш. | уступ | 0,02 | 0,62 | 0,62 | |
| С2 | увеличив. | уступ | 0,02 | 0,74 | 0,74 | |
| А3 | увеличив. | вал | 0,24 | 1,15 | 1,15 | |
| А4 | увеличив. | вал | 0,24 | 0,12 | 0,12 | |
| А5 | уменьш. | уступ | 0,02 | 0,52 | 0,52 | |
| А6 | уменьш. | вал | 0,24 | 1,15 | 0,46 |

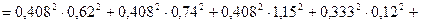

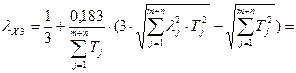
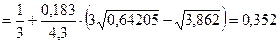 .
.
По формуле 13 определим расчётное значение допуска замыкающего звена в зависимости от назначенных допусков составляющих звеньев
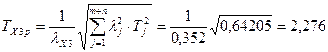 мм
мм
Расчетный допуск больше исходного, а должен лежать в пределах 2÷1,8. Поэтому выбираем в качестве регулировочного составляющее звено А6 = 206 мм, меняем допуск в сторону уменьшения, выбирая из 12 квалитета ТА6 = 0,46 мм [7, табл. 1.8], и записываем в табл. 4. Повторяем расчёт допуска замыкающего звена.
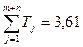 ,
, 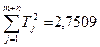 ,
, 
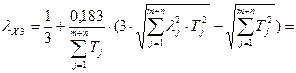
 .
.
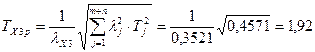 мм
мм
Полученное значение расчётного допуска замыкающего звена укладывается в заданный диапазон. Нужно уточнить предельные отклонения. По формуле 11 определим коэффициент относительной асимметрии αХ3 для замыкающего звена
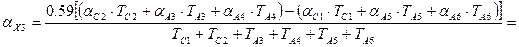
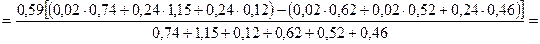
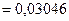
Определим значение среднего отклонения ЕХ3ср расчётного допуска замыкающего звена по формуле 8

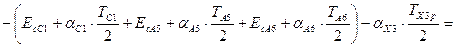
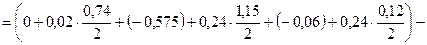
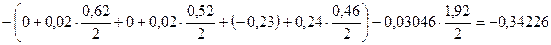
По формулам 15 и 16 определяем расчётные верхнее ESX1p и нижнее EIX1p предельные отклонения замыкающего звена
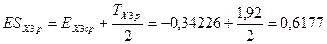

Нижнее предельное отклонение EIX3р = – 1,30226 меньше нижнего допустимого отклонения, равного – 1 (см. исходный данные). Необходимо изменить основное предельное отклонение регулирующего звена. В данный момент размер регулирующего звена в записи выглядит так А6=206 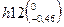 и основное предельное отклонение h = 0. Выбираем для регулирующего звена основное предельное отклонение a = – 0,38 мм. Тогда размер будет выглядеть А6=206
и основное предельное отклонение h = 0. Выбираем для регулирующего звена основное предельное отклонение a = – 0,38 мм. Тогда размер будет выглядеть А6=206 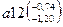 и ESA6 = –0,38, EIA6= –0,84, EcA6 = –0,61. Повторим расчёт предельных отклонений замыкающего звена.
и ESA6 = –0,38, EIA6= –0,84, EcA6 = –0,61. Повторим расчёт предельных отклонений замыкающего звена.
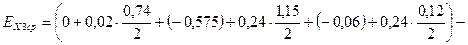
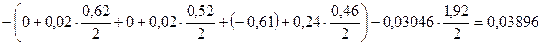
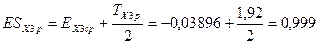
 .
.
Результат удовлетворяет исходным данным: 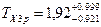 мм
мм
Рекомендуемая литература: [1, с. 382–387], [8, с. 6–85], [13, с. 96–140], [16, с. 126–142, 447–456], [30, с. 288–290], [33, с. 35–72], [47, с. 294–318],
Контрольные вопросы:
1. Назначение размерного анализа сборочной единицы.
2. Что такое размерная цепь?
3. Структура размерных цепей.
4. Какое звено размерной цепи называют замыкающим?
5. Какими бывают составляющие звенья размерной цепи?
6. Особенности расчета размерных цепей на минимум-максимум и вероятностным методом.
7. Принципы выявления замыкающих звеньев размерных цепей в сборочных единицах.
8. Виды распределений действительных размеров.
9. Дать определения допуску, предельным отклонениям, основному предельному отклонению, среднему предельному отклонению.
Дата добавления: 2015-09-07; просмотров: 2546;
