Второй закон Кирхгофа

В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех его участках

,

где n – число источников ЭДС в контуре;
m – число элементов с сопротивлением R_к в контуре;
U_к = R_кI_к – напряжение или падение напряжения на к-м элементе контура.

Для схемы (рис. 1) запишем уравнение по второму закону Кирхгофа:

E = U_R + U₁.

Если в электрической цепи включены источники напряжений, то второй закон Кирхгофа формулируется в следующем виде: алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС равна нулю

.

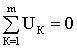При записи уравнений по второму закону Кирхгофа необходимо:

1) задать условные положительные направления ЭДС, токов и напряжений;

2) выбрать направление обхода контура, для которого записывается уравнение;

3) записать уравнение, пользуясь одной из формулировок второго закона Кирхгофа, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с обходом контура, и со знаком «минус», если они противоположны.

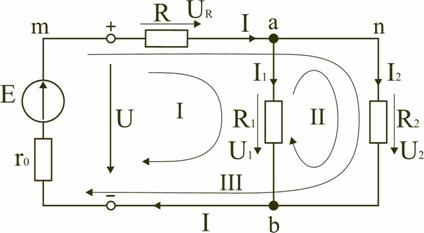Рис.2

Запишем уравнения по II закону Кирхгофа для контуров электрической схемы (рис. 2):

контур I: E = RI + R₁I₁ + r₀I,

контур II: R₁I₁ + R₂I₂ = 0,

контур III: E = RI + R₂I₂ + r₀I.

В действующей цепи электрическая энергия источника питания преобразуется в другие виды энергии. На участке цепи с сопротивлением R в течение времени t при токе I расходуется электрическая энергия

W = I²Rt.

Скорость преобразования электрической энергии в другие виды представляет электрическую мощность

.

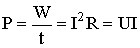Из закона сохранения энергии следует, что мощность источников питания в любой момент времени равна сумме мощностей, расходуемой на всех участках цепи.

.

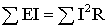Это соотношение (1.8) называют уравнением баланса мощностей. При составлении уравнения баланса мощностей следует учесть, что если действительные направления ЭДС и тока источника совпадают, то источник ЭДС работает в режиме источника питания, и произведение E I подставляют в (1.8) со знаком плюс. Если не совпадают, то источник ЭДС работает в режиме потребителя электрической энергии, и произведение E I подставляют в (1.8) со знаком минус. Для цепи, показанной на рис. 1.2 уравнение баланса мощностей запишется в виде:

EI = I²(r₀ + R) + I₁²R₁ + I₂²R₂.

Схемы соединения приёмников электрической цепи.

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением R_экв, и вся схема представляется в виде схемы на рис. 1.3, где R=R_экв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.