Задача Коши для обыкновенных дифференциальных уравнений

Требуется найти решение и(х)задачи Коши

и' = f(x, u), u(x₀)= u₀ (3)

При изучении численных методов для задачи Коши будем считать, что она имеет единственное решение в замкнутой прямоугольной области D = {а ≤ х ≤ b, с ≤ и ≤ d}. Пусть требуется найти решение задачи (3) на отрезке [а, b]. Введем на отрезке [а, b] сетку 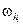, следующим образом:

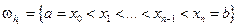
где точки х_i, i = 0, 1, ..., n называются узловыми точками или узлами сетки, 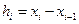, i = 1, ..., n − шагами сетки; п − натуральное число. Если h_i = h = const, то такую сетку будем обозначать 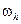, и называть равномерной. Сетку 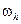можно задать так:

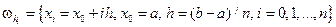
В дальнейшем будем пользоваться равномерной сеткой 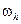, с шагом h.

Пусть u_i = u(x_i) − значение точного решения (3) в точке x_i,а у_i − соответствующее приближенное значение, полученное с помощью рассматри­ваемого численного метода.