Исходное дифференциальное уравнение
ý - y - 2*sin(x) = 0;
Рис 5. Форма для условия задачи.
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
this->Hide();
}
private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {
double f1,x, y1;
double h = Convert::ToDouble(textBox1->Text);
double b = Convert::ToDouble(textBox2->Text);
double y = Convert::ToDouble(textBox3->Text);
x = 0;
y1 = y;
chart1->Series[0]->Points->Clear();
chart1->Series[1]->Points->Clear();
do
{
f1 = y - 2*sin(x);
x = x+h;
y = y+f1*h;
chart1->Series[0]->Points->AddXY(x, y);
chart1->Series[1]->Points->AddXY(x,f1);
}
 while (x<=b);
while (x<=b);
}};}};}
Рис 6. Форма для автора.
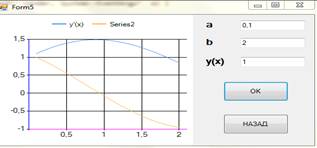
Рис 7. Форма для отображения результатов моделировния.
Язык программирования C#
private void button1_Click(object sender, EventArgs e)
{
double h = 0.01;
double y = 0;
double b = 2;
double x = 0;
double y1 = 4;
do
{
double f = y + 2*Math.Sin(x);
x = x + h;
y = y1 + f * h;
chart1.Series[0].Points.AddXY(x, y);
chart1.Series[1].Points.AddXY(x, f);
y1 = y;
}
while (x <= b);
}
// foreach (DataPoint p in chart1.Series[0].Points)
// {
// Вывожу Х в лог
// textBox1.AppendText("X=" + p.XValue.ToString());
// textBox1.AppendText(Environment.NewLine);
// listBox1.Items.Add("X=" + p.XValue.ToString());
// }
// Y является массивом, поэтому пробегаю по массиву
// foreach (DataPoint yp in chart1.Series[0].Points)
// {
//Вывожу Y
// textBox1.AppendText("Y=" + yp.ToString());
// textBox1.AppendText(Environment.NewLine);
// listBox1.AppendText("Y=" + yp.ToString());
// listBox1.AppendText(Environment.NewLine);
// listBox2.Items.Add("Y=" + yp.ToString());
// }
// }
private void chart1_Click(object sender, EventArgs e)
{
}
private void button2_Click_1(object sender, EventArgs e)
{
Close();
} }}
Пример 2.
Условия задачи:Исследовать объект, динамика которого представляется дифференциальным уравнением
ý - y - a*sin(x) = 0;
Цель занятия: получить практические навыки исследования систем (объектов), динамика которых описывается дифференциальными уравнениями 1-го порядка при изменении параметра «а»
Задачи занятия:
1. Разработка алгоритма в виде блок- схемы.
2. Построение графиков кривых y=f(x), ý = f(x) =y(x) при параметрах a-var
Рис 8. Титульный лист Рис. 9. Условия задачи
Рис 10. Автор программы
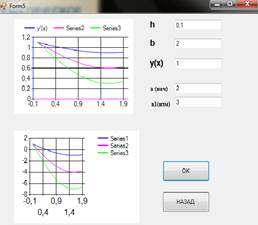
Рис. 11. Результаты исследования.
Листинг программы
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
this->Hide();
}
private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {
double f1,f2,x, y1;
double h = Convert::ToDouble(textBox1->Text);
double b = Convert::ToDouble(textBox2->Text);
double y2 = Convert::ToDouble(textBox3->Text);
double a = Convert::ToDouble(textBox4->Text);
double a1 = Convert::ToDouble(textBox5->Text);
x = 0;
// double y1 = y2;
int a3=a;
//for int i=0;i<=1;i++)
//{
chart1->Series[0]->Points->Clear();
chart1->Series[1]->Points->Clear();
chart1->Series[2]->Points->Clear();
chart2->Series[0]->Points->Clear();
chart2->Series[1]->Points->Clear();
chart2->Series[2]->Points->Clear();
//}
do
{
// for (int i=1;i<=5;i++)
// {
a3=a;
f1 = y2 - a3*sin(x);
// int i=0;
double y = y2+f1*h;
//int i=0;
chart1->Series[0]->Points->AddXY(x, y);
chart2->Series[0]->Points->AddXY(x,f1);
a3=a3+a1;
f1 = y2 - a3*sin(x);
y = y2+f1*h;
chart1->Series[1]->Points->AddXY(x,y);
chart2->Series[1]->Points->AddXY(x,f1);
a3=a3+a1;
f1 = y2 - a3*sin(x);
y = y2+f1*h;
chart1->Series[2]->Points->AddXY(x,y);
chart2->Series[2]->Points->AddXY(x,f1);
//y=y2;
x = x+h;
}
while (x<=b);
x=0;
}
private: System::Void chart2_Click(System::Object^ sender, System::EventArgs^ e) {
}
private: System::Void textBox1_TextChanged(System::Object^ sender, System::EventArgs^ e) {
}
};
}
Дата добавления: 2015-09-07; просмотров: 1343;
