Решение задачи. 1. Определяем число независимых уравнений для решения задачи, которое равно числу независимых контуров

1. Определяем число независимых уравнений для решения задачи, которое равно числу независимых контуров. Между числом независимых контуров, узлов и ветвей любой схемы существует следующая зависимость

К=В-У+1, (7.9)

где К- число контуров; В- число ветвей; У- число узлов.

В нашем примере К=6-4+1=3. Следовательно, используя равенство (7.9), необходимо составить три независимых уравнения. В это равенство входит алгебраическая сумма давлений, создаваемая вентилятором. В нашем примере это вентилятор ВОД-21 с углом установки лопаток рабочего колеса 40⁰. Для решения задачи необходимо аппроксимировать характеристику вентилятора. В области промышленного использования характеристика вентилятора достаточно точно описывается равенством

H=a-b*Q², (7.10)

где а- коэффициент, имеющий размерность и смысл депрессии;

b- коэффициент, характеризующий внутреннее сопротивление вентилятора.

Возьмем две точки, расположенные на концах рабочей характеристики вентилятора ВОД-21 при 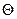=40⁰

Рис.6.17 К пояснению аппроксимации аэродинамической характеристики вентилятора ВОД-21 с углом установки лопаток рабочего колеса 40⁰

Точка 1 на графике соответствует координатам Н₁=400, кг/м² Q₁ =43 м³/с, а точка 2

Н₂=200 кг/м², Q₁ =64 м³/с. Тогда можно составить два уравнения

400=а-b 43²

200=а-b 64²

Из этих равенств определяем, а=564, b=0.089 и характеристика вентилятора опишется равенством

Н=564-0.089 Q² (7.11)

Обозначим контура. Контур 1-й 0-1-3-4-5-0, контур 2-й 1-2-3-1, контур 3-й 2-4-3-2.

Составим расчетные уравнения для обозначенных контуров:

Для первого контура

∆q₁=- 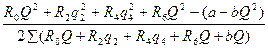(7.12)

После незначительных преобразований, получим для первого контура

∆q₁=- 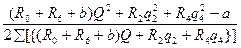(7.13)

В нашем примере R₀+R₆+b=0.154 кµ. Подставляя значения постоянных в равенство (6.88) получим формулу для расчета поправок в первом контуре

∆q₁=- 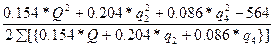(7.14)

Составим уравнение для расчета поправок во втором контуре

∆q₂= 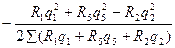(7.15)

Подставляя значения сопротивлений в равенство (7.15), получим

∆q₂= 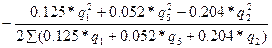(7.16)

Составим уравнение для расчета поправок в третьем контуре

∆q₃= 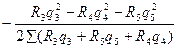(7.17)

После подстановки значений аэродинамического сопротивления ветвей, получим

∆q₃= 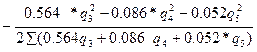(7.18)

Принимаем первоначальное, произвольное распределение воздуха:

Q=45м³/с; q₁₌25 м³/с; q₂=20 м³/с; q₃₌15 м³/с; q₄=30 м³/с; q₅=10 м³/с;

По формуле (7.14) определяем величину ошибки для первого контура. В нашем примере она будет равна 3.4 м³/с. Исправляем первоначально принятые значения воздуха в первом контуре

Q=48.4 м³/с, q₂=23.4 м³/с; q₄ 33.4 м³/с;

По формуле (7.16) определяем величину ошибки для второго контура. В результате расчета получим ∆q₂=3.3 м³/с. Исправляем первоначально принятые значения расходов воздуха во втором контуре

q₁=28.3 м³/с, q₅=13,3 м³/с, q₂=20,1 м³/с.

По формуле (7.18) определяем величину ошибки для третьего контура. В результате расчета получим ∆q₃=-1.8 м³/с. Исправляем первоначально принятые значения воздуха

q₃=13,2 м³/с, q₄=35,2 м³/с, q₅=15,1 м³/с.

Далее, снова выполняем расчет величины ошибки для всех контуров и исправляем расходы воздуха. Расчет повторяется несколько раз, пока последующие расходы воздуха будут отличаться от предыдущих расходов с требуемой степенью точности.

Результаты расчетов сводим в табл. 7.1.