Способ последовательных приближений

Уравнения (6.57), (6.58) являются уравнениями двух гипербол. Уравнение (6.57) описывает гиперболу с действительной полуосью «b» параллельной оси «x» и центром, смещенным на –1 по оси «y» (рис.6.15).

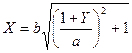(6.57)

Уравнение (6.58) описывает гиперболу с действительной полуосью «С»параллельной оси «Y» и центром, смещенным на –1 по оси «X»

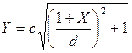(6.58)

Координаты точки пересечения этих гипербол являются корнями системы (6.57) (6.58). Решая эту систему методом последовательных приближений, задаемся первоначальным значением Х=Х₀ и, подставляя его в уравнение (6.58), находим приближенное значение Y=Y₁. Подставляя значение Y₁ в уравнение (6.57), находим более точное значение Х=Х₁, которое в свою очередь подставляем в уравнение (6.58), определяя более точное значение Y=Y₂. Эта операция повторяется до совпадения двух последующих значений с требуемой степенью точности.

Рис.6.15 Схема сходимости при определении корней системы уравнений (6.57) (6.58)

На рис.6.15 стрелками показана схема сходимости к точному корню системы. Из уравнений (6.57) (6.58) и рис. 6.15 видно, что имеет смысл принимать первоначальное значение Х₀>b, а Y₀>c, что избавит от лишних вычислений.