Особенности излучения паров и реальных газов
Газы, как и твердые тела, обладают способностью излучать и поглощать лучистую энергию, но для различных газов эта способность различна. Одно- и двухатомные газы (кислород, водород, азот и др.) для тепловых лучей практически прозрачны (диатермичны). Значительной излучательной и поглощательной способностью обладают трех- и многоатомные газы, например, углекислота (СО2), водяной пар (Н2О), сернистый ангидрид (SO2), аммиак (NH3) и др. По сравнению с твердыми телами излучение и поглощение газов имеет ряд особенностей.
Излучение и поглощение газов носит характер избирательного (селективного) излучения, т. е. газы излучают и поглощают энергию лишь в определенных интервалах длин волн, в так называемых полосах, расположенных в различных частях спектра, в то время как твердые тела в большинстве случаев излучают и поглощают лучистую энергию длин волн от 0 до ¥. Например, для углекислоты и водяного пара наиболее важное значение имеют следующие полосы:
| Углекислота СО2 | Водяной пар Н2О | |
| 1-ая полоса | l=2,36¸3,02 мкм | l=2,24¸3,27 мкм |
| 2-ая полоса | l=4,01¸4,80 мкм | l=4,80¸8,50 мкм |
| 3-ая полоса | l=12,5¸16,5 мкм | l=12,0¸25,0 мкм |
Твердые тела для тепловых лучей непрозрачны, поэтому можно считать, что излучение и поглощение лучистой энергии происходит в поверхностном слое.
Излучение и поглощение газов носит объемный характер, так как в нем участвуют все микрочастицы газа, заключенные в рассматриваемом объеме. При прохождении тепловых лучей через газ их энергия вследствие поглощения уменьшается. Количество поглощенной энергии зависит от числа встречаемых тепловым лучом молекул газа, т. е. определяется длиной пути луча l и давлением газа P. Поэтому поглощательная способность газа Аl для какой-нибудь длины волны является функцией произведения Pl.
Кроме того, поглощательная способность газа зависит от его температуры Т. Поэтому можно записать
Аl=¦1(T, Pl). (4.98)
Согласно закону Кирхгофа, тела, поглощающие лучистую энергию, обладают способностью ее излучать. Наличие излучения газа доказывается следующим образом.
Пусть имеется некоторое полое тело с одинаковой температурой по всей внутренней поверхности. В отношении лучистого обмена внутренняя поверхность такого тела будет находиться в состоянии динамического равновесия: каждый его элемент излучает столько энергии, сколько он сам получает от остальной части поверхности.
Если заполнить это полое тело газом, температура которого равна температуре тела, то при наличии газа каждый элемент поверхности будет излучать такое же количество энергии, как и раньше, но от остальной части поверхности сам он будет получать меньше, так как часть этой энергии поглощается газом. Так как температура газа равна температуре стенок, т. е. соблюдается тепловое равновесие газа и стенок, недостающая энергия может быть получена только за счет собственного излучения. Поэтому можно считать, что излучаемая газом энергия и энергия, поглощаемая им, равны между собой. Известно, что при полосовых спектрах излучения, которые характерны для газов, закон Стефана — Больцмана неприменим. Например, согласно опытным данным для углекислого газа и водяного пара излучательная способность может быть определена по формулам:
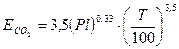 ; (4.99)
; (4.99)
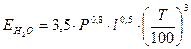 . ( 4.100)
. ( 4.100)
Иначе говоря, каждый газ имеет свой собственный закон излучения, что, естественно, затрудняет теплотехнические расчеты. Поэтому в основу практических расчетов по излучению положен все же закон 4-ой степени абсолютной температуры — закон Стефана — Больцмана:
Ег=εг·с0(Т/100)4, (4.101)
где Ег — количество энергии излучения газа в единицу времени;
εг — степень черноты газа.
Учитывая, что степень черноты представляет отношение излучательных способностей рассматриваемого и абсолютно черного тел, из уравнений (4.99 и 4.100) можно сделать вывод, что εг=ƒ(Т, Pl).
Для смеси газов степень черноты не равна сумме степеней черноты компонентов, а определяется, например, для смеси из двух газов:
εг=ε1+ε2-Δeг.
Это обстоятельство определяется тем, что полосы излучения и поглощения для компонентов частично совпадают, что предопределяет взаимное поглощение энергии компонентов.
Формулой (4.101) определяется количество энергии, излучаемой газом в пустоту, которую можно рассматривать как абсолютно черное пространство при Т=0°К. В действительности газ всегда огражден твердой поверхностью (оболочкой), температура которой выше 0°К, а степень черноты меньше 1. Такая поверхность имеет собственное излучение, которое частично поглощается газом, а частично — отражается. Отраженная оболочкой энергия частично поглощается газом, а частично — отражается. Результирующий тепловой поток при теплообмене излучением между газом и оболочкой определится разностью между тепловым потоком, излучаемым газом на оболочку, и частью излучения оболочки, которое поглощается газом. Так как газ поглощает селективно, то степень черноты газа εг и его поглощательная способность Аг не равны между собой, как у твердых тел. Кроме того, при наличии излучающего газа эффективная степень черноты оболочки εэф.с больше степени черноты оболочки в диатермичной среде и приближенно может быть вычислена по формуле εэф.с=(εс+1)/2. Окончательно расчетная формула теплообмена между газом и оболочкой имеет вид
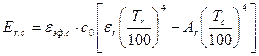 . (4.102)
. (4.102)
Формула (4.102) справедлива для лучистого теплообмена, когда длина пути луча l в любом направлении одна и та же, т. е. для полусферы. В газовых телах другой формы длина пути в разных направлениях различна. В этом случае вводится понятие средней длины пути луча, которая определяется из следующего соотношения:
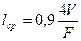 , (4.103)
, (4.103)
где V — объем газа, м3;
F — поверхность его оболочки, м2.
Дата добавления: 2015-10-13; просмотров: 943;
