Элементы комбинаторики
В разделе “Комбинаторный анализ” изучаются понятия, позволяющие определить без прямого пересчета различные возможные комбинации конечного числа элементов некоторого множества.
Принцип умножения:
Пусть нужно последовательно выполнить 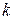 действий. Если первое действие можно выполнить
действий. Если первое действие можно выполнить 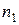 различными способами, второе –
различными способами, второе – 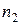 различными способами и так до
различными способами и так до 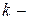 го действия, которое можно выполнить
го действия, которое можно выполнить 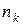 различными способами, то все
различными способами, то все 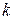 действий можно выполнить
действий можно выполнить 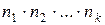 различными способами.
различными способами. 
Принцип сложения:
Если два действия взаимно исключают друг друга, причем одно из них можно выполнить 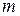 различными способами, а другое –
различными способами, а другое – 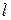 различными способами, то какое-либо одно из них можно выполнить
различными способами, то какое-либо одно из них можно выполнить 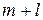 различными способами.
различными способами.
Перестановкой из 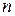 элементов называют упорядоченное расположение этих элементов в определенной линейной последовательности.
элементов называют упорядоченное расположение этих элементов в определенной линейной последовательности.
Различные перестановки из 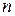 элементов отличаются порядком их следования. Число перестановок из
элементов отличаются порядком их следования. Число перестановок из 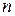 элементов:
элементов:
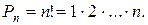
Из трех элементов 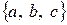 можно составить
можно составить 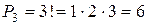 перестановок:
перестановок:
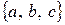 ,
, 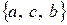 ,
, 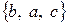 ,
, 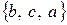 ,
, 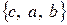 ,
, 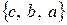 .
.
Размещением из 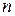 элементов по
элементов по 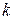 элементов называют произвольное упорядоченное
элементов называют произвольное упорядоченное 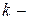 элементное подмножество
элементное подмножество 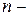 элементного множества.
элементного множества.
Различные размещения из 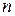 элементов по
элементов по 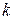 отличаются друг от друга набором элементов и (или) порядком их следования. Число размещений из
отличаются друг от друга набором элементов и (или) порядком их следования. Число размещений из 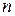 элементов по
элементов по 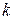 элементов:
элементов:
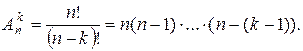
Из трех элементов 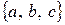 можно составить
можно составить 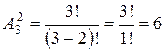 двухэлементных размещений:
двухэлементных размещений:
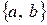 ,
, 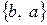 ,
, 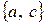 ,
, 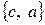 ,
, 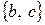 ,
, 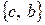 .
.
Сочетанием из 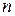 элементов по
элементов по 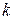 называют произвольное неупорядоченное
называют произвольное неупорядоченное 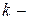 элементное подмножество
элементное подмножество 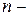 элементного множества.
элементного множества.
Различные сочетания из 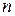 элементов по
элементов по 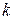 отличаются друг от друга набором элементов. Число сочетаний из
отличаются друг от друга набором элементов. Число сочетаний из 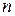 элементов по
элементов по 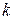 элементов:
элементов:
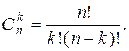
Замечание: 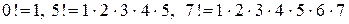 и т.д.
и т.д.
Из трех элементов 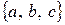 можно составить
можно составить 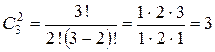 двухэлементных сочетаний:
двухэлементных сочетаний:
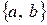 ,
, 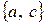 ,
, 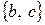 .
.
Комбинации 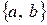 и
и 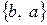 представляют собой одно сочетание.
представляют собой одно сочетание.
| Пример. | Сколько существует различных трехзначных чисел? |
Решение.
Каждую цифру числа можно выбрать определенным числом способов: первую – девятью (все цифры подходят, кроме нуля, т.к. иначе это будет не трехзначное число), вторую – десятью и третью – десятью способами. По принципу умножения: 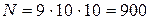 .
.
| Пример. | Сколькими способами могут распределиться призовые места на чемпионате по футболу, в котором участвуют 12 команд? |
Решение.
По принципу умножения на первое место могут претендовать 12 команд, на второе – 11 (одна команда заняла первое место), на третье – 10. Следовательно, общее число способов 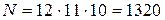 .
.
С помощью числа размещений:
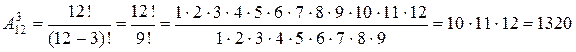 .
.
| Пример. | Сколькими способами можно заполнить лотерейный билет 5 из 36? |
Решение.
Поскольку при заполнении билета не важен порядок следования чисел, то количество способов вычисляют по формуле числа сочетаний:
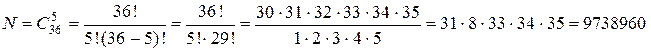 .
.
2. Виды событий
Под событием в теории вероятностей понимают всякий факт, который в результате испытания может произойти или не произойти.
| Например: | событие  – появление герба при подбрасывании монеты,
событие – появление герба при подбрасывании монеты,
событие 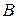 – попадание в мишень при выстреле,
событие – попадание в мишень при выстреле,
событие 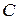 – извлечение туза из колоды карт,
событие – извлечение туза из колоды карт,
событие 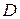 – первенцем в определенной семье является мальчик,
событие – первенцем в определенной семье является мальчик,
событие 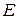 – 1 августа в Донецке будет дождь. – 1 августа в Донецке будет дождь.
|
Достоверным 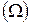 называют событие, которое в результате опыта непременно должно произойти.
называют событие, которое в результате опыта непременно должно произойти.
Невозможным (Æ) называют событие, которое в результате данного опыта не может произойти.
Случайным называется событие, которое в результате данного опыта может произойти или не произойти.
Несколько событий образуют полную группу событий в данном опыте, если в результате опыта непременно должно появиться хотя бы одно из них.
| Например: | события 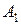 , , 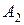 , , 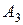 образуют полную группу, если:
событие образуют полную группу, если:
событие 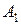 – менее двух опечаток на странице,
событие – менее двух опечаток на странице,
событие 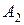 – одна опечатка на странице,
событие – одна опечатка на странице,
событие 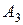 – более одной опечатки на странице. – более одной опечатки на странице.
|
Несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе.
| Например: | при выборе одной карты будут несовместными события:
событие 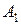 – появление туза,
событие – появление туза,
событие 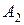 – появление дамы,
событие – появление дамы,
событие 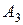 – появление валета,
событие – появление валета,
событие 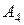 – появление десятки. – появление десятки.
|
События называются совместными в данном опыте, если появление одного из них не исключает появления остальных.
Несколько событий называются равновозможными в данном опыте, если в силу симметрии нет оснований считать, что одно из событий является объективно более возможным, чем другие.
| Например: | равновозможными при одном подбрасывании монеты будут такие события:
событие 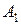 – появление “орла”,
событие – появление “орла”,
событие 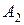 – появление “решки”. – появление “решки”.
|
Если несколько событий образуют полную группу, несовместны и равновозможны, то их называют случаями или исходами.
Случай называют благоприятствующим событию  , если появление этого случая влечет за собой наступление данного события.
, если появление этого случая влечет за собой наступление данного события.
Например, при подбрасывании игральной кости событию  – “появление четного числа очков” благоприятствуют три исхода
– “появление четного числа очков” благоприятствуют три исхода 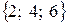 .
.
Противоположными в данном опыте называют два несовместных события  и
и 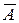 , которые образуют полную группу.
, которые образуют полную группу.
| Например: | событие  – попадание при выстреле,
событие – попадание при выстреле,
событие 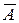 – промах. – промах.
|
Дата добавления: 2015-10-13; просмотров: 1541;
