Модель фильтрационного течения

Сложный и нерегулярный характер структуры порового пространства не позволяет изучать движение флюидов в нем прямым решением уравнений движения вязкой жидкости для каждого порового канала или трещины. Однако, известно, что с увеличением числа отдельных микродвижений, составляющих макроскопическое фильтрационное движение, начинают проявляться суммарные статистические закономерности, характерные для движения в целом и несправедливые для одного или нескольких поровых каналов. Это характерно для систем с большим числом однородных элементов, слабо связанных между собой. Такие системы могут быть описаны как некоторые сплошные среды, свойства которых не выражаются непосредственно через свойства составляющих элементов, а являются осредненными характеристиками достаточно больших объемов среды. Так, в гидродинамике не изучается движение отдельных молекул, а вводятся осредненные термо-динамические параметры жидкости как сплошной среды. При этом предполагается, что любой объем осреднения намного превосходит элементарный линейный размер (межмолекулярное расстояние) и содержит достаточно большое число элементарных элементов (молекул), а сам намного меньше характерного макрообъема, н.п. диаметра трубопровода. Аналогично этому теория фильтрации строится на представлении породы и заполняющей ее флюида сплошной средой. Это означает, что элементы системы флюид - порода считаются физически бесконечно малыми, но достаточно великими по сравнению с размерами пустот и зерен породы. При этом предполагается, что в одном и том же элементарном объеме содержатся одновременно порода и флюид.

Известно, что в механике сплошных сред течение жидкостей и газов описывается тремя законами сохранения: массы, количества движения или импульса, энергии. При исследовании фильтрационного течения в подземной гидромеханике используется только первые два уравнения, а изменением температуры флюида пренебрегается по причине малых скоростей течения и значительного теплообмена со скелетом пород, вследствие значительной поверхности контакта, которые практически не меняют своей температуры из-за большой своей теплоёмкости. Т.о. процесс течения предполагается изотермическим. Необходимо отметить, что в отдельных случаях (тщательное изучение призабойной зоны, использование термических методов интенсификации добычи флюидов) используют и общую постановку - с учётом изменения температуры не только флюида, но и породы.

Для процессов, происходящих в нефте-газовых, пластах при разработке, характерно наличие периодов изменения параметров течения во времени (пуск и остановка скважин, проведение работ по интенсификации притока). Такие процессы называют неустановившимися (нестационарными), а сами модели течения нестационарными. Те же модели, которые описывают процессы не зависящими от времени, называют стационарными (установившимися). При этом в данных моделях по причине малости изменения скорости и значительного преобладания сил сопротивления над инерционными, уравнение количества движения используется независящим от времени и пренебрегается изменением импульса по пространству.

Моделирование фильтрационного течения по отношению к пространственному изменению параметров может проводиться в: одномерной постановке, т.е. когда параметры являются функцией только одной переменной - это течение по прямой или кривой; двухмерной постановке - течение по плоскости и трехмерной - течение в пространстве.

Флюиды различны по степени сжимаемости. Так природный газ способен значительно изменять свой объём при изменении давления, вода и нефть в довольно значительном диапазоне давлений (приблизительно до 20МПа) практически несжимаемы, а при высоких давлениях обладают упругими свойствами. В связи с указанными факторами различают модели сжимаемой, несжимаемой и упругой среды. Построение каждой из указанной модели требует привлечения эмпирических уравнений состояния, т.е. соотношений связывающих изменение объёма с изменением давления.

В области контакта флюидов при вытеснении одного другим или при выделении одного флюида из другого в каждом микрообъёме содержится два или больше флюидов, занимающих отдельные четко различимые объёмы (пузырьки газа в жидкости, капли или плёнки в газе) и взаимодействующих на поверхностях раздела. Такие системы называют многофазными (двух, трёх и т.д.) в отличие от многокомпонентных смесей (природный газ, нефть), в которых взаимодействие происходит на молекулярном уровне и поверхности раздела выделить нельзя. В гидродинамике такие среды называют однофазными или гомогенными.

В процессе движения флюиды испытывают различные деформации (сжатие, кручение, растяжение и т.д.) при изменении нагрузки( трение соседних объёмов, внешние силы), которая, отнесённая к единице площади, получила название напряжения. Само соотношение, связывающее деформацию или скорость изменения деформации с напряжением, называется реологическим соотношением или законом. Наиболее часто, применительно к жидкостям, для описания действия касательных напряжений t_xy на сдвиговую деформацию применяют соотношение Ньютона 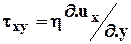, гдеu_x- скорость в направлении х; у- направление перпендикулярное х; h - коэффициент динамической вязкости. Довольно часто движение флюидов не подчиняется данному закону, н.п. при трогании пластовой нефти требуется некоторое, отличное от нулевого, напряжение, чтобы разорвать образованные пластовой водой коллоидные структуры. Такие среды называются неньютоновскими, а модель - моделью неньютоновского течения.