НАУЧНАЯ ГРАФИКА
Компьютерная графика представляет значительный интерес для научных исследований. В частности, она выступает как средство формирования научной документации с использованием специальной нотации - математических знаков, индексов, шрифтов и т.п. В последнее время ученые чаще стали обращаться к имитационному моделированию на компьютере.
В компьютерной графике большое значение имеют методы и способыгеометрического моделирования. Модели, геометрические преобразования составляют в настоящее время основу теории компьютерной графики и геометрического моделирования.Аналитические модели - это набор чисел, логических параметров, играющих роль коэффициентов в уравнениях, которые задают графический объект заданной формы. Например, аналитической моделью окружности на плоскости в параметрической форме являются уравнения
x=x0+R-cosA,
y=y0+R-sinA,
где х0, у0 - координаты центра, R - радиус, А - угол. Параметрическое задание образов широко применяется в машинной графике и геометрии. Изображение окружности можно осуществить установкой последовательных точек (близко расположенных), изменяя генерирующий параметр А от 0 до 360°.
Координатные модели - это массивы координат точек, принадлежащих объектам. Например, поверхность задается массивом точек Z = f (x, у) на координатной сетке [хi, yj}. Если точки в модели расположены в том же порядке, что и на линии образа, то модели называют упорядоченными. Помимо координат, в модели могут быть указаны дополнительные характеристики проекции касательных или нормальных векторов.
Приближенные модели содержат аппроксимации кривых методами вычислительной геометрии. Например, изображение гладких кривых можно осуществить ломаными линиями: линейными, параболическими или сплайнами. Используя вышеперечисленные геометрические модели, можно создавать различные демонстрационные картины. Например, модель Солнечной системы для наглядности удобно представить в динамической форме. Организуем движение точки (Земли) по окружности, в центре которой размещается круг (имитация Солнца). Установку точки на орбите осуществим по параметрическим формулам окружности:
X0 = 320 + r1∙sin(A1);
Y0 = 240 + rl ∙cos(Al),
где r1 - радиус орбиты Земли, А1 - параметрический угол, меняющийся от 0 до 360°. Чтобы организовать движение, достаточно в цикле устанавливать точку с координатами (x0, у0) для всех углов А1, принимающих значения от 0 до 360° с шагом h. Аналогичная процедура справедлива и для второй точки (Луны), которая изображается по подобным формулам, в которых центр орбиты (Земля) является подвижным:
х = х0 + r ∙ sin(A);
у = у0 + r ∙ cos(A),
где r - радиус орбиты Луны, А - угол вращения.
Контрольные вопросы и упражнения
1. Составьте каким-либо средством машинной графики бордюры каждого типа симметрии из следующих элементарных мотивов, рис. 2.21.
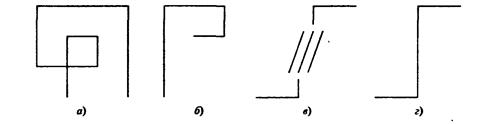
Рис. 2.21.
2. Постройте орнаменты различного типа симметриииз выбранного произвольного элементарного мотива каким-либо средством машинной графики.
3. Задана высота (м) над уровнем моря вершин: Мак-Кинли - 6200, Логан - 6100, Элберт - 440, Робсон - 4000, Митгелл - 2000. Составьте по этим данным столбчатую диаграмму.
4. По данным упражнения 3 составьте круговую диаграмму.
5. Постройте график функции у = x sin (1/x).
6. Создайте мультипликацию: вращение электрона в модели атома.
7. Изобразите шестиугольную призму.
8. Подготовьте иллюстрацию ко Дню учителя.
9. Организуйте в школе (вузе) компьютерный вернисаж.
Дата добавления: 2015-10-13; просмотров: 775;
