ИЗОБРАЗИТЕЛЬНАЯ ГРАФИКА

При работе с художественной графикой, включая компьютерную графику, необходимо знать следующие понятия.

Композиция - строение, соотношение и взаимное расположение частей, сосредоточие идейно-творческого начала, позволяющего автору произведения искусства целенаправленно организовывать главное и второстепенное и добиваться максимальной выразительности содержания и формы в их образном единстве.

Законы композиции:

1) закон цельности: во-первых, наличие конструктивной идеи, объединяющей в единое целое все компоненты произведения; во-вторых, связь и взаимная согласованность всех элементов композиции; в-третьих, неповторимость элементов композиции;

2) закон контрастов: контраст света и тени определяет форму предметов; контрасты величин, построения сюжета определяют композицию. Правила композиции:

1) передача ритма: ритм в удачной композиции одновременно расчленяет компоненты произведения и объединяет их;

2) композиционный центр: выделяется объемом, освещенностью и другими средствами, действующими в соответствии с основными законами композиции.

Мера - характеризует общие принципы строения, целостность предмета,лежит воснове ритма, гармонии, ансамбля в архитектуре.

Симметрия - одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости. Симметрия в композиции создается уравновешенностью ее частей по массам, тону, цвету и форме. Симметрия (геометрическая) - свойство геометрических фигур при котором каждая пара соответственных точек лежит на одном перпендикуляре к данной плоскости по разные стороны и на одинаковом расстоянии от нее.

Пропорция - определенное соотношение частей между собой, соразмерность.

Ритм - равномерное чередование каких-нибудь элементов.

Гармония - соразмерность частей, слияние различных компонентов объекта в единое органичное целое. В истории эстетики гармония - существенная характеристика прекрасного.

Перспектива - искусство изображать на плоскости трехмерное пространство в соответствии с тем кажущимся изменением величины, очертаний, четкости предметов, которое обусловлено степенью отдаленности их от точки наблюдения.

При моделировании графических объектов на экране дисплея используют разные методы и способы представления изображений. Можно выделить два принципа моделирования - случайный и детерминированный. На их основе строятся технологии в изобразительной графике, в которой условно можно выделить три направления: художественное, иллюстративное и демонстрационное.

Объектами художественной графики выступают различные узоры, шрифты и другие изображения. При работе с изображениями широко используют простые мотивы и разнообразный геометрический материал. В частности, простые геометрические фигуры в различных сочетаниях и способах размещения (вложения, вращения, симметрии) используются в «живых картинках» для получения муарового эффекта. Удачное сочетание случайного и упорядоченного в любой пропорции с технологиями расположения графических объектов позволяет создавать художественный дизайн.

Самые простые узоры - бордюры - представляют бесконечный ряд равных плоских фигур, расположенных друг за другом таким образом, что элементарная конечная фигура переносится вдоль одного измерения бесконечно. Помимо элементарного мотива для получения бордюра необходимо выбрать группу симметрии бордюра и задать конкретные образующие этой группы из следующего набора движений плоскости:

• параллельный перенос;

• центральная симметрия;

• осевая симметрия;

• скользящая симметрия.

Для бордюр существует четыре абстрактные группы симметрии, которые определяют семь типов симметрии бордюр:

1) один параллельный перенос;

2) одна скользящая симметрия;

3) две осевые симметрии;

4) две центральные симметрии;

5) одна осевая и одна центральная симметрия;

6) один параллельный перенос и одна осевая симметрия;

7) три осевые симметрии.

Существует несколько способов построения бордюр по заданному элементарному мотиву и системе образующих ее группы симметрии. Рассмотрим наиболее простые из них. Первый способ основан на простом переборе элементов группы - на элементарный мотив действуют поочередно всеми элементами группы симметрии бордюра. Множество полученных образов и будет представлять собой требуемый бордюр. Этот способ неудобен тем, что на каждом этапе необходимо представить очередной элемент группы в виде композиции подходящих степеней образующих.

Второй способ более предпочтителен. На элементарный мотив действуют одним из образующих. Затем на новую фигуру, составленную из исходного мотива и его образа, действуют любым образующим, который не отображает эту фигуру на себя. Получается фрагмент бордюра, состоящий из предыдущей фигуры и ее образа.

Продолжая этот процесс можно построить любую конечную часть бордюра. Преимущество этого способа заключается в том, что на каждом этапе мы будем иметь дело с конкретной симметрией, с нахождением образа конкретной фигуры.

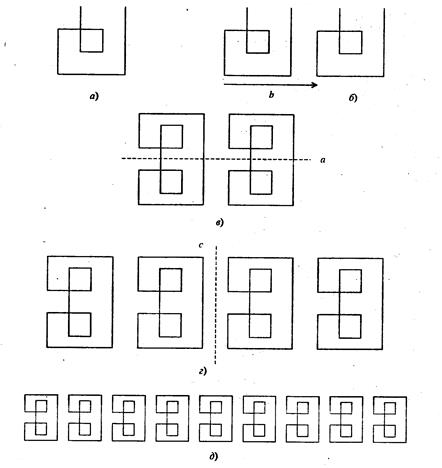
Рис. 2.16. Схема построения бордюра

Рассмотрим, например, процесс построения бордюр с помощью образующих шестого типа симметрии. Создадим элементарный мотив узора (рис. 2.16, а) и определим образующие: параллельный перенос зададим векторомb, (рис. 2.16, б) осевую симметрию прямой а (рис. 2.16, в)

Процесс получения бордюра с помощью заданных образующих вторым из описанных выше способом проиллюстрирован поэтапно. На элементарный мотив действуем параллельным переносом на вектор b, см. схему б. Получим фигуру, состоящуюиз элементарного мотива и его образа. На новую фигуру действуем осевой симметрией с осью а. Получим фигуру, изображенную на схеме в, на которую действуем параллельным переносом 2b. В результате получим новую фигуру, см. схему г. Продолжая этот процесс, получаем фрагмент бордюра нужной длины.

Бордюры используются для окантовки обоев, ковров; для настенной росписи, украшающей здания, подземные переходы; в виде металлических решеток для ограждения парков, мостов и садов и пр.

Более зрелищны, привлекательны и интересны по построению орнаменты. Любой орнамент получается переносом узора с помощью двух параллельных переносов, заданных неколлинеарными векторами. Для любого орнамента можно найти сетку, узлы которой составляют вполне определенную систему равных точек орнамента. Различают пять типов плоских решеток: квадратная, прямоугольная, гексагональная, ромбическая и косая. Тип плоской решетки определяет характер переносной симметрии данного орнамента.

В простейшем случае орнамент характеризуется только переносной симметрией. Для построения такого орнамента надо выбрать соответствующую плоскую решетку, заполнить элементарную ячейку решетки определенным рисунком и затем многократно повторить этот рисунок за счет переносов ячейки без изменения ее ориентации. Для построения более сложных по композиции орнаментов рисунок элементарной ячейки заполняется из основного (элементарного) мотива с помощью образующих этого типа симметрии плоских орнаментов. Существует 17 типов симметрии плоских орнаментов, которые определяются следующим образом:

1) два параллельных переноса:

2) три центральных симметрии;

3) две осевые симметрии и параллельный перенос;

4) две скользящие симметрии с параллельными осями;

5) осевая и скользящая симметрии с параллельными осями;

6) симметрия относительно четырех сторон прямоугольника;

7) одна осевая и две центральные симметрии;

8) две скользящие симметрии с перпендикулярными осями;

9) две осевые симметрии с перпендикулярными осями и одна центральная симметрия;

10). центральная симметрия и вращение на 90°;

11) симметрия относительно трех сторон прямоугольного равнобедренного треугольника;

12) осевая симметрия и вращение на 90°;

13) два вращения на 120°;

14) осевая симметрия и вращение на 120°;

15) симметрия относительно равностороннего треугольника;

16) центральная симметрия и вращение на 120°;

17) симметрия относительно трех сторон прямоугольного треугольника с углом 30°.

Несколько слов о частных случаях орнаментов. Бесконечная плоская фигура Ф называется плоским орнаментом, если выполняются следующие условия: 1) среди перемещений, отображающих Ф на себя, существуют неколлинеарные параллельные переносы; 2) среди всех векторов (параллельных переносов), отображающих Ф на себя, существует вектор наименьшей длины. Фигуру называют линейным орнаментом, если плоская фигура отображается сама на себя при параллельных переносах только одного направления (и противоположного ему), причем среди этих переносов существует перенос наименьшей длины.

Большой интерес представляют паркеты. Паркетом называется разбиение плоскости на многоугольники, при котором каждые два многоугольника либо не пересекаются, либо имеют ровно одну общую вершину, либо имеют общую сторону, причем объединение сторон всех многоугольников является плоским орнаментом. Паркет называется правильным, если все многоугольники разбиения правильные (возможно с различным числом сторон) и любую величину паркета можно перевести в любую другую величину некоторым перемещением, отображающим весь паркет на себя.

Интересны орнаменты, заполненные одинаковыми фигурками без промежутков. Фигурку такого орнамента можно создать с помощью геометрических преобразовании на основе гексагональной сетки.

Процесс моделирования орнаментов на экране компьютера аналогичен моделированию бордюр: после получения повторяющейся фигурки из элементарного мотива с помощью образующих данного орнамента вывод на экран происходит циклическим изменением координат в двух направлениях. При моделировании орнаментов на основе различных плоских решеток без «заполнения» их элементарной ячейки получаются паркеты. Для осуществления компьютерного моделирования графического объекта выбирают подходящее программное инструментальное средство - графический редактор (систему), например, PaintBrash, CorelDraw и т.п., в котором допустимы все возможности, необходимые для описанной работы. Иногда бывает полезным осуществить построение графического образа программированием (на одном из языков программирования) с использованием графических библиотек.

Узор на плоскости получается из элементарного мотива с помощью образующих элементов его группы симметрии. Для бордюр существует 7 различных наборов образующих его групп симметрии, для орнаментов - 17. Чтобы построить узор на компьютере, необходимо

1) создать элементарный мотив узора (в графическом редакторе,на языке программирования, сканированием с листа бумаги);

2) выбрать и задать образующие;

3) построить образы каждой точки элементарного мотива по его образующим, т.е. получить из элементарного мотива изображение конечной повторяющейся фигуры;

4) средствами имеющегося компьютера и программного обеспечения размножить получившийся «шаблон» (фигурку), циклически меняя координаты в одном или в двух направлениях.

В художественной графике часто обращаются к узорам, получаемым в результате «интерференции» при наложении каких-либо семейств кривых. При пересечении, например, двух семейств прямых под заданным углом получаются «муаровые» эффекты, рис. 2.17.

Моделирование муаровых узоров представляет простой, но занимательный процесс, в котором основная роль принадлежит зрительному восприятию исследователя, который, меняя параметры семейств кривых и их способы пересечения, добивается наилучшей в смысле гармонии красоты узоров.

Используя принцип муаровых узоров, можно моделировать на экране дисплея фейерверки. Простейший одиночный фейерверк можно изобразить по следующему принципу. Из фиксированной точки (x, у) строят отрезки прямых в точку, задаваемую случайным образом и случайным цветом. Возникающие одиночные фейерверки, пересекаясь друг с другом, создают красивые картинки.

Узоры можно моделировать с помощью простых мотивов, в частности, штрихованного угла. Штрихованный угол задается координатами трех точек и изображается семейством отрезков, соединяющих точки разбиения сторон угла с одинаковыми номерами. Подобные мотивы удобно оформлять в виде подпрограммы, а затем использовать при моделировании различных изображений.

. Рис. 2.17. Муаровый pop

Сочетание случайного и упорядоченного в любой пропорции при изображении графических объектов дает эффект. Например, на основе простого мотива - угла, вершина которого находится на горизонтальной прямой, - можно изобразить «лес». При упорядоченном размещении «деревьев» имеем «посадку».

Подобные технологии широко используют в иллюстративной графике. В настоящее времяиллюстративная графика, в первую очередь, связана с изображением графического материала в издательских системах.

Иллюстративный материал - схемы, эскизы, географические карты, чертежи и др. -можно создавать различными графическими редакторами, системами. Здесь важна легкость и быстрота формирования и преобразования графических изображений для тех или иных приложений. В последнее время большой интерес вызывает иллюстративный материал, представленный в демонстрационной, динамической форме.

Демонстрационная графика связана с динамическими объектами. Втехнологииизображения динамических объектов используют три основных способа: рисование -стирание, смену кадров (страниц), динамические образы.

Достаточно просто организовать перемещение фрагмента рисунка на экране. Для этого надо

• создать этот фрагмент в нужном месте экрана;

• стереть фрагмент, рисуя его цветом фона или используя процедуру очистки экрана;

• снова нарисовать фрагмент в другом месте экрана, и так далее.

Еще один способ организации движения объектов на экране, широко применяющийся в компьютерных играх, связан с использованием нескольких экранных страниц. В любой момент времени одну из страниц можно сделать видимой и посмотреть ее содержимое на экране. Визуальная страница обычно пассивна, т.е. на ней нельзя выполнять графические процедуры. Другую страницу можно объявить активной. Активная страница невидима для пользователя, но на ней можно подготовить другой рисунок. Меняя страницы ролями, можно создать мультипликационный сюжет

В обучающих программах и в компьютерных играх часто используют динамические образы (в том числе спрайты). При этом используют динамическую память для хранения прямоугольных фрагментов рисунков и последующего вывода их в нужное место экрана.