Квадратичные формы. Некоторые свойства линейных пространств
Некоторые свойства линейных пространств
Утверждение 1. В произвольном линейном пространстве нулевой элемент — единственный.
Утверждение 2. В произвольном линейном пространстве нулевой элемент равен произведению произвольного элемента на действительное число 0.
Утверждение 3. В произвольном линейном пространстве каждому элементу отвечает единственный противоположный элемент.
Утверждение 4. В произвольном линейном пространстве противоположный элемент произвольного элемента x равен произведению x на действительное число -1.
Утверждение 5. В произвольном линейном пространстве для любых двух произвольных элементов x и y существует и единственна разность:
x-y = x+(-1) ·y.
Квадратичные формы
Квадратичной формой от 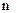 переменных
переменных 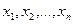 называется сумма
называется сумма
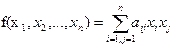 , где
, где 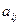 - элементы квадратной матрицы
- элементы квадратной матрицы
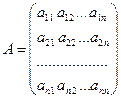 , называемой матрицей квадратичной формы.
, называемой матрицей квадратичной формы.
 Квадратичная форма называется симметрической, если
Квадратичная форма называется симметрической, если 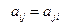 . В этом случае
. В этом случае 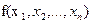
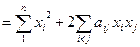 . Например, при
. Например, при 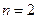 , имеем
, имеем
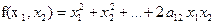 , где
, где 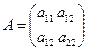 .
.
Симметрическая квадратичная форма называется положительно определенной, если выполнены неравенства
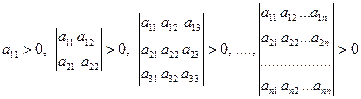
Симметрическая квадратичная форма называется отрицательно определенной, если выполнены неравенства
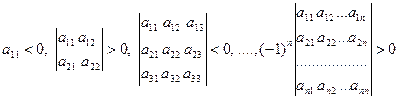
Пример. Записать матрицу квадратичной формы 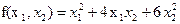 .
.
Решение. 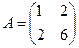
Пример. Записать канонический вид квадратичной формы 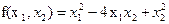
Решение. Преобразуем 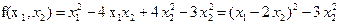 . Обозначим
. Обозначим 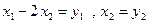 . Тогда канонический вид квадратичной формы запишется так
. Тогда канонический вид квадратичной формы запишется так
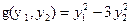 .
.
Пример. Записать матрицу квадратичной формы 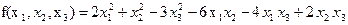 .
.
Решение. 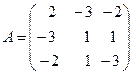
Пример. Положительно определенная квадратичная форма может иметь вид
1. 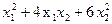 ; 2.
; 2. 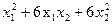 ; 3.
; 3. 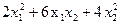 ; 4.
; 4. 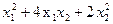
Решение. Выписываем матрицы квадратичных форм и соответствующие определители
1. 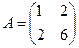 ,
, 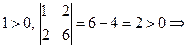 положительно определена.
положительно определена.
2. 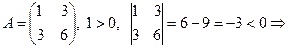 не явл.пол.опред.
не явл.пол.опред.
3. 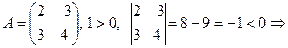 не явл.пол.опред
не явл.пол.опред
4. 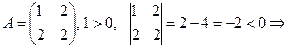 не явл.пол.опред
не явл.пол.опред
Ответ. 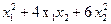
СВОДКИ ФОРМУЛ
Дата добавления: 2015-10-13; просмотров: 582;
