Расчёт элементов при поперечном изгибе.
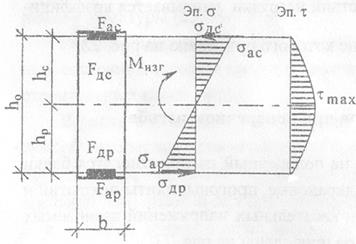
К конструкциям, работающим на поперечный изгиб, относятся балки стропильные, подстропильные и подкрановые, прогоны, плиты покрытий и др. Расчётные эпюры нормальных и касательным напряжений изгибаемых армированных деревянных элементов приведены на рис. 4.4.
1. По первой группе предельных состояний рассчитывается прочность и устойчивость балки:
1) на действие нормальных напряжений в древесине:
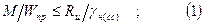

2) на действие нормальных напряжений в арматуре:
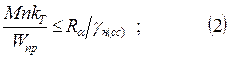
3) устойчивость плоской формы деформирования, проверяется при шаге связей по сжатому поясу при lр>70b2/h ;
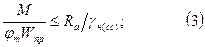
4) на действие касательных напряжений в древесине
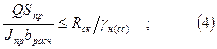
5)
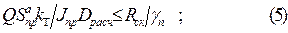 |
на действие касательных напряжений в клеевом шве, соединяющем арматуру с древесиной
6) на действие главных растягивающих напряжений под углом к волокнам на расстоянии Х1= 0.85 от опоры
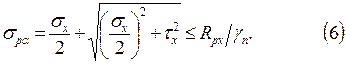 |
II. По второй группе предельных состояний определяется прогиб балки:
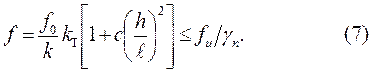 |
Балки с рациональным армированием проверяются в месте отгиба на расстоянии х от опоры по сечению с m=0. В формулах (1) - (7) использованы следующие обозначения:
M и Q - расчётный изгибающий момент и поперечная сила;
Rи и Rск - расчётное сопротивление древесины изгибу и скалыванию;
Ra - расчётное сопротивление арматуры;
f - полный прогиб; f0=КРl 3/(EJпр) - прогиб от поперечной нагрузки;
К - коэффициент, зависящий от вида балки и характера нагрузки;
K=5/384 - для равномерно распределенной нагрузки;
c - коэффициент, принимается по табл. Е3, приложения СП 64.13330. 2011;
fи - предельный прогиб, принимаемый по табл. 19 СП 64.13330. 2011;
Dрасч - расчётная поверхность сдвига арматуры, равная 0,9 суммы периметров клеевого шва, соединяющего древесину с арматурой, т.е. Dрасч =0.9;
kт=1+0.67qТ/q - коэффициент, учитывающий увеличение напряжений в арматуре при постоянных или длительно действующих нагрузках вследствие перераспределения усилий;
q - полная расчётная нагрузка на балку;
qТ - составляющая полной нагрузки от постоянной и длительно действующих нагрузок;
gн(сс) - коэффициент надёжности по сроку службы сооружения, учитывающий величину принятого расчётного сопротивления древесины R (по табл. 3, 4 и 6) посредством деления R/gн(сс) на величину по табл. 12 по СП 64.13330. 2011;
sx- нормальные напряжения вдоль волокон древесины по оси арматурных стержней в рассматриваемом сечении, равные sх=Мх/Wпр;
Мх - изгибающий момент на расстоянии 0.85 от опоры; Wпр - приведённый момент сопротивления в рассматриваемом сечении; txy - скалывающее напряжение на уровне нейтральной оси, равное txy=QxS/Jb;
Qx - поперечная сила в рассматриваемом сечении, a - угол, определяющий направление главных растягивающих напряжений, равный a=36±2° ;
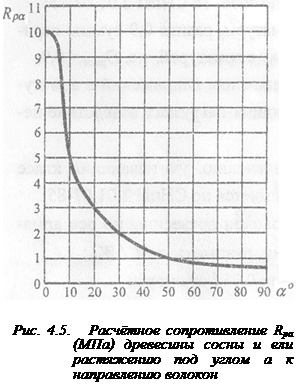
Rрa - расчётное сопротивление древесины растяжению под углом a, принимается по графику (рис. 4.5).
 В случае если условие (6) не выполняется,т.е. необходимо поперечное армирование приопорной зоны на длине Х от опор, такое армирование целесообразно проводить наклонно вклеенными (a = 36°) или поперечными стержнями. Если поперечные стержни ставятся конструктивно (см. п. 5.10) [15], то площадь сечения наклонных стержней приближенно можно определить по формуле:
В случае если условие (6) не выполняется,т.е. необходимо поперечное армирование приопорной зоны на длине Х от опор, такое армирование целесообразно проводить наклонно вклеенными (a = 36°) или поперечными стержнями. Если поперечные стержни ставятся конструктивно (см. п. 5.10) [15], то площадь сечения наклонных стержней приближенно можно определить по формуле:
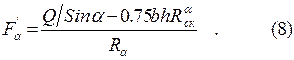
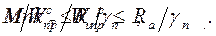
При расчёте сечений с одиночным армированием (стержни в растянутой зоне) проверяется прочность древесины сжатой зоны и арматуры растянутой зоны. В этом случае формулы (1) и (2) имеют вид:
Дата добавления: 2015-10-13; просмотров: 1481;
