Классификация точек покоя

Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами

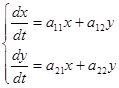
Характеристическое уравнение этой системы имеет вид:

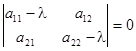
Рассмотрим следующие возможные случаи:

1) Корни характеристического уравнения действительные, отрицательные и различные.

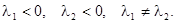
Точка покоя 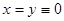будет устойчива. Такая точка покоя называется устойчивым узлом.

2) Корни характеристического уравнения действительны и

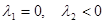или .

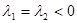В этом случае точка покоя также будет устойчива.

3) Хотя бы один из корней 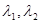положителен.

В этом случае точка покоя 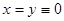неустойчива, и такую точку называют неустойчивым седлом.

4) Оба корня характеристического уравнения положительны .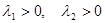

В этом случае точка покоя 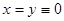неустойчива, и такую точку называют неустойчивым узлом.

Если полученного решения 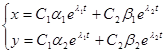системы исключить параметр t, то полученная функция 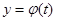дает траекторию движения в системе координат XOY.

Возможны следующие случаи:

b b

a a

Устойчивый узел. Неустойчивый узел. Седло.

5) Корни характеристического уравнения комплексные .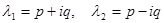

Если р = 0, т.е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову. Такая точка покоя называется центром.

Если p < 0, то точка покоя устойчива и называется устойчивым фокусом.

Если p > 0, то точка покоя неустойчива и называется неустойчивым фокусом.