Нормальные системы обыкновенных дифференциальных уравнений

Определение. Совокупность соотношений вида:

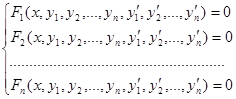
где х- независимая переменная, у₁, у₂,…,у_n – искомые функции, называется системой дифференциальных уравнений первого порядка.

Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.

Такая система имеет вид:

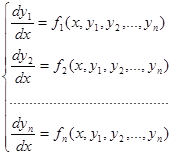(1)

Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.

Теорема. (Теорема Коши). Если в некоторой области (n-1) –мерного пространства функции 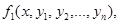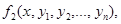… 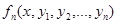непрерывны и имеют непрерывные частные производные по 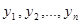, то для любой точки 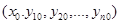этой области существует единственное решение

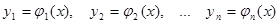
системы дифференциальных уравнений вида (1), определенное в некоторой окрестности точки х₀ и удовлетворяющее начальным условиям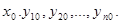

Определение. Общим решениемсистемы дифференциальных уравнений вида (1) будет совокупность функций 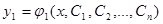, , 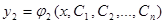… , 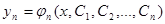которые при подстановке в систему (1) обращают ее в тождество.