Основные свойства определенного интеграла

1 При перестановке пределов интегрирования знак определённого интеграла изменяется на противоположный.

2 Постоянный множитель подынтегрального выражения можно выносить за знак определённого интеграла.

3 Определённый интеграл суммы функций равен сумме определённых интегралов этих функций.

Например, вычислить определённый интеграл:

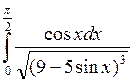
Решение. Этот интеграл можно вычислить, введя следующую замену переменой:

9-5sin x = t, тогда d(9-5sinx) = d t,

или –5 cos x d x =d t, откуда: Cos x d x = - 1/5 d t

При замене переменной в определенном интеграле поменяются и границы интегрирования. Новые границы интегрирования найдем из подстановки, то есть из равенства

9-5sin x = t, полагая в нем x = 0, а затем, соответственно 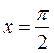, получим: t = 9 и t = 4. Это можно записать короче так: .

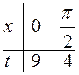Итак, 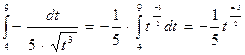(4,9)= .

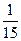Вопросы для повторения

1 Дайте определение первообразной функции.

2 Что такое неопределённый интеграл от данной функции?

3 Что называется интегрированием функции?

4 Основные свойства неопределённого интеграла.

5 В чём состоит геометрический смысл неопределённого интеграла.

6 Основные формулы интегрирования.

7 Способ подставки и способ интегрирования по частям.

8 Определённый интеграл.

9 Свойства определённого интеграла

10 Формула Ньютона – Лейбница.

11 Геометрический смысл определённого интеграла.