Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.
Например,
∫ (4х³ − 15х² +14х−3 )dx = ∫ 4x³dx − ∫ 15x²dx + ∫ 14xdx − ∫ 3dx = 4 x4 /4 − 15 x³/3 + 14 x²/2 − 3x + c = = x4 − 5x³ + 7x ²− 3x + C;
∫(х2+1)2dx=∫(х4+2х2+1)dx=∫х4dx+2∫x2dx+∫dx=x5/5+2x3/3+x+C;
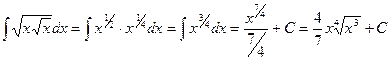 .
.
3.2. Интегрирование способом подстановки
При интегрировании подстановкой вводится новая переменная с таким расчётом, чтобы получить один из табличных интегралов. Найдя интеграл по новой переменной, надо возвратиться к первоначальной переменной и дать окончательный ответ.
Указать общее правило для выбора подстановки нельзя, так как этот выбор в каждом отдельном случае зависит от вида подынтегральной функции.
Например, найти следующие интегралы:
1 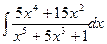 .
.
Решение. Применим подстановку 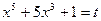 , где t – новое переменное. Продифференцируем обе части равенства:
, где t – новое переменное. Продифференцируем обе части равенства:
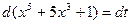 или
или 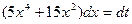 .
.
Теперь можно записать
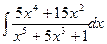 =
= 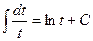 .
.
Возвращаясь к первоначальной переменной, получим окончательно:
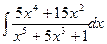 =
= 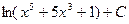
Приступая к интегрированию рациональных функций, следует посмотреть, нельзя ли подынтегральную функцию привести к такому виду, чтобы в числителе была производная от знаменателя, тогда можно будет сразу записать ответ.
2  .
.
Решение. Находим производную знаменателя: 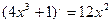 . Сравнивая это выражение с числителем, замечаем, что там нет сомножителя 12. Если умножить числитель дроби на 12, а за знак интеграла вынести сомножитель 1/12, то получим:
. Сравнивая это выражение с числителем, замечаем, что там нет сомножителя 12. Если умножить числитель дроби на 12, а за знак интеграла вынести сомножитель 1/12, то получим:
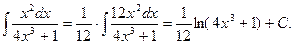
3 
Решение. Полагаем 5х=t, тогда 5dx = dt и dx =1/5dt;
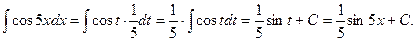
4 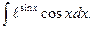
Решение. Положим sinx=t, тогда cosxdx=dt;
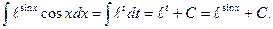
Дата добавления: 2015-10-13; просмотров: 905;
