Введение.
Аспирант кафедры Константин Андреевич Тимолянов
Литература: Трофимов А.И. «Курс физики»
Савельев И.В. «Курс общей физики»
Лекция 1. Элементы кинематики.
[1]. гл. 1
План лекции
1. Введение.
2. Основные кинематические понятия и характеристики.
3. Нормальное, тангенциальное и полное ускорения.
4. Угловая скорость, угловое ускорение.
Введение.
Физику можно назвать наукой о наиболее общих свойствах и законах движения материи.
В настоящее время известны два вида материи - вещество (атомы, молекулы, тела) и поле (гравитационное, электромагнитное); наблюдается взаимное превращение различных видов материи ( 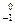 e+
e+ 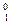 e®2g, возможен обратный процесс).
e®2g, возможен обратный процесс).
Материя находится в непрерывном движении, под которым понимается всякое изменение вообще. Движение - неотъемлимое свойство материи, которое неуничтожимо, как сама материя.
Материя существует и движется в пространстве и во времени, которые являются формами бытия материи.
Форм движения материи много. Предмет «Физика» изучается в порядке усложнения форм движения материи и делится на следующие разделы: механика, молекулярная физика, электричество и магнетизм, оптика, физика атома и атомного ядра.
“Физика” – от греческого “физис” – природа. Физику подразделяют на так называющую классическую физику и физику квантовую.
Классической называется та физика, начало которой было положено Ньютоном и создание которой было завершено в начале XX столетия.
Ньютоновская механика оказалось настолько плодотворной, что у физиков сложилось представление о том, что любое физическое явление можно объяснить с помощью ньютоновских законов.
Однако такие блестящие достижения физики как открытие электрона (1897г.), создание электронной теории, теории относительности, квантовой теории требовали пересмотра установившихся физических понятий и представлений.
В физике необходимо различать скалярные и векторные величины. Скалярные величины полностью характеризуются численными значениями и единицей измерения; могут иметь положительное или отрицательное численное значение (исключение составляет температура по шкале Кельвина).
Векторная величина полностью характеризуется численным значением, единицей измерения и направлением. Для указания на векторный характер физической величины над обычным ее обозначением ставится стрелка. Векторная величина геометрически изображается вектором, т.е. отрезком, имеющим определенное направление и длину.
Математические операции над векторными величинами подчиняются особым закономерностям.
1.Сложение векторов
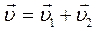
а) 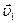 и
и 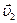 сонаправлены
сонаправлены

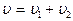
б) 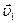 и
и 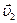 направлены противоположно
направлены противоположно

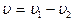
в) 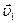
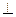
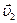 , используется правило параллелограмма
, используется правило параллелограмма 
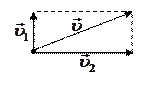
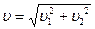 .
.
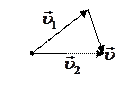 2.Вычитание векторов
2.Вычитание векторов
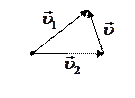
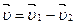
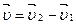
3. Производная вектора
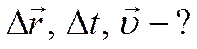
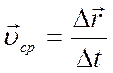 ,
, 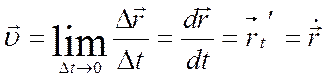
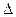 – знак изменения,
– знак изменения,
d – знак бесконечно малого изменения.
4. Понятие интеграла.
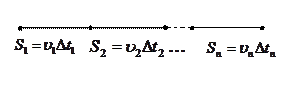
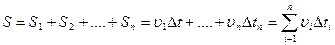 .
.
Если n – велико, а 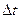 - мало, то
- мало, то 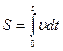 .
.
Дата добавления: 2015-09-07; просмотров: 993;
