Формализация базы знаний

На этапе формализации базы знаний осуществляется выбор метода представления знаний.

Рассмотрим классификацию методов представления знаний (рис. 2.4).

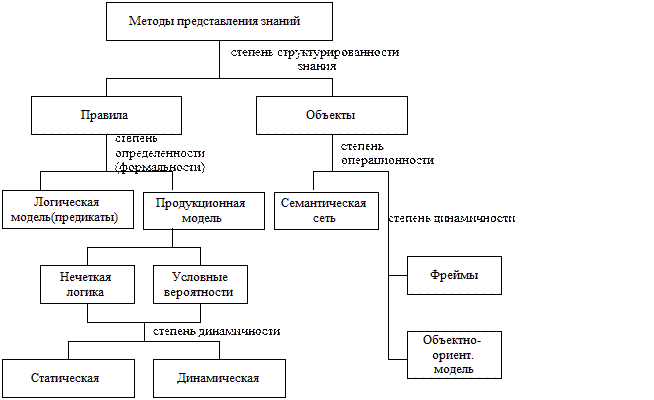
Рис. 2.4. Классификация методов представления знаний

Известно, что используемые в экспертных системах данные являются плохо формализуемыми. При более структурированных знаниях выбирают правила, как средство представления знаний. В противном случае переходят к объектно-ориентированному моделированию.

При формализации базы знаний посредством правил используются следующие методы представления знаний:

· Логическая модель описывает как объекты, так и правила с помощью предикатов первого порядка и является строго формализованной моделью с универсальным дедуктивным и монотонным методом, использующей логический вывод "от цели к данным".

· Продукционная модель позволяет использовать эвристические методы вывода для правил и может обрабатывать неопределенности в виде условных вероятностей или коэффициентов уверенности, а также выполнять монотонный или немонотонный вывод.

При формализации базы знаний посредством объектов существуют следующие методы:

· Семантическая сеть отображает разнообразные отношения объектов.

· Фреймовая модель как частный случай семантической сети использует для реализации операционного знания присоединенные процедуры.

· Объектно-ориентированная модель как развитие фреймовой модели, реализуя обмен сообщениями между объектами, в большей степени ориентирована на решение динамических задач и отражение поведенческой модели.

Рассмотрим подробнее все вышеуказанные методы представления знаний.

Логическая модель предполагает унифицированное описание объектов и действий в виде предикатов первого порядка. Под предикатом понимается логическая функция на N аргументах (признаках), которая принимает истинное или ложное значение в зависимости от значения аргумента. Пример фрагмента базы знаний (отбор претендентов на вакансии) на языке логического программирования ПРОЛОГ представлен на рис. 3.2 (обозначения: ":-" – "если"; "," – "и"; "." – "конец утверждения").

vibor(Fio,Dolgnost):-

pretendent(Fio, Obrazov, Stag),

vacancy(Dolgnost, Obrazov, Opyt),

Stag>=Opyt.

pretendent("Иванов","среднее", 10).

pretendent("Петров","высшее", 12).

vacancy("менеджер", "высшее", 10).

vacancy("директор", "высшее", 15).

Рис. 3.2. Пример фрагмента базы знаний на языке ПРОЛОГ

Механизм вывода использует дедуктивный перебор фактов по принципу "сверху - вниз", "слева - направо" или обратный вывод методом поиска в глубину. Так, в ответ на запрос vibor(X,Y) получим: X="Петров", Y="менеджер".

Правила могут связываться в цепочки. Для логической модели характерна строгость формального аппарата получения решения. Однако полный последовательный перебор всех возможных решений может приводить к комбинаторным взрывам, в результате чего поставленные задачи могут решаться недопустимо долго. Кроме того, работа с неопределенностями знаний должна быть запрограммирована в виде самостоятельных метаправил, что на практике затрудняет разработку баз знаний с помощью логического формализма.

Продукционная модель основана на применении эвристических методов представления знаний, позволяющих настраивать механизм вывода на особенности проблемной области и учитывать неопределенность знаний. Продукционные модели используются для решения более сложных задач, по сравнению с задачами, которые решают логические модели.

В продукционной модели основной единицей знаний служит правило вида: "если <посылка>, то <заключение>", с помощью которого могут быть выражены пространственно-временные, причинно-следственные, функционально-поведенческие (ситуация – действие) отношения объектов. Правилами могут быть описаны и сами объекты: "объект – свойство" или "набор свойств – объект", хотя чаще описания объектов фигурируют только в качестве переменных ("атрибут – значение") внутри правил. В основном продукционная модель предназначена для описания последовательности различных ситуаций или действий и в меньшей степени может быть использована для структурированного описания объектов.

Продукционная модель предполагает более гибкую организацию работы механизма вывода по сравнению с логической моделью. Так, в зависимости от направления вывода возможна как прямая аргументация (прямой вывод, т.е. от данных к цели), так и обратная (обратный вывод, т.е. от целей к данным). Прямой выводиспользуется в продукционных моделях при решении, например, задач интерпретации, когда по исходным данным нужно определить сущность некоторой ситуации, или в задачах прогнозирования, когда из описания некоторой ситуации требуется вывести все следствия. Обратный выводприменяется, когда нужно проверить одну или несколько гипотез на соответствие фактам, например, в задачах диагностики.

Отличительной особенностью продукционной модели является также способность осуществлять выбор правил из множества возможных на данный момент времени в зависимости от определенных критериев, например, важности, трудоемкости, достоверности получаемого результата и других характеристик проблемной области. Такая стратегия поиска решений называется поиском в ширину. Для ее реализации в описание продукций вводятся предусловия и постусловия в виде

< A, B, C → D, E >,

где импликация С → D представляет собственно правило; А – предусловие выбора класса правил; B – предусловие выбора правила в классе; Е –
постусловие правила, определяющее переход на следующее правило.

В пред- и постусловиях могут быть заданы дополнительные процедуры, например, по вводу и контролю данных, математической обработке и т. д. Введение пред- и постусловий позволяет выбирать наиболее рациональную стратегию работы механизма вывода, существенно сокращая перебор относящихся к решению правил.

Правила могут быть простыми и обобщенными. Простые правила описывают действия над единичными объектами, обобщенные правила используются для класса объектов (аналогично правилам языка ПРОЛОГ).

Для обработки неопределенностей знаний продукционная модель использует методы обработки условных вероятностей Байеса (Байесовский подход)? или методы нечеткой логики Заде.

Байесовский подход предполагает априорное ( независимо от опыта, до опыта) начальное задание предполагаемых гипотез (значений достигаемых целей) или вероятностей, которые последовательно уточняются в пользу или против гипотез, в результате чего формируются апостериорные (конечные) вероятности. Апостериорная вероятность гипотезы рассчитывается через апостериорные шансы, которые в свою очередь получаются перемножением априорных шансов на факторы достаточности или необходимости всех относящихся к гипотезе свидетельств в зависимости от их подтверждения или отрицания со стороны пользователя. Свидетельства рассматриваются как независимые аргументы на дереве целей.

Существенным недостатком байесовского подхода к построению продукционной базы знаний является трудоемкость статистического оценивания априорных шансов и факторов достаточности и необходимости.

Подход на основе нечеткой логики. Более простым, но менее точным методом оценки достоверности используемых знаний является применение нечеткой логики, в которой вероятности заменяются на экспертные оценки определенности фактов и применения правил (факторы уверенности). Факторы уверенности могут рассматриваться и как весовые коэффициенты, отражающие степень важности аргументов в процессе вывода заключений. Итоговые факторы уверенности получаемых решений главным образом отражают порядок достоверности результата, а не его точность, что вполне приемлемо во многих задачах (приложение 1).

Факторы уверенности (cf) измеряются по некоторой относительной шкале, например, от 0 до 100. Множество возможных значений некоторой переменной с различными факторами уверенностей для каждого значения составляет нечеткое множество вида: { x1 cf1, x2 cf2, ... , xN cfN }, причем фактор уверенности в общем виде задается функцией принадлежности Заде, например, как представлено на рис. 2.5. Так, для рентабельности 6,7 % получаем оценку в виде нечеткого множества {"неудовлетворительно" cf = 66, "удовлетворительно" cf = 33}).

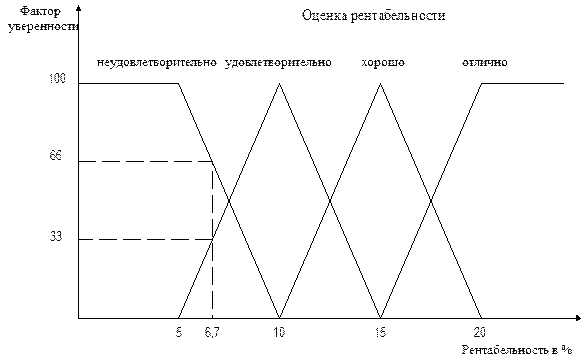Рис. 2.5. Функции принадлежности нечеткого множества
"Оценка рентабельности"

Предполагается, что оценка факторов уверенностей исходных данных задается пользователем при описании конкретной ситуации, а факторы уверенности применения правил определяются инженерами знаний совместно с экспертами при наполнении базы знаний.

При объединении факторов уверенности конъюнктивно или дизъюнктивно связанных аргументов используются следующие формулы:

Конъюнкция (А и В) : min (cfA, cfB) или cfA*cfB/100.

Дизъюнкция (А или В): max (cfA, cfB) или cfA + cfB - cfA*cfB/100.

Объединение факторов уверенности в посылках правил осуществляется чаще всего (например, в программном средстве GURU) по формулам "min/max", а левых и правых частей правил и результатов нескольких правил соответственно по формулам "произведение" и "сумма". Для объединения результатов нескольких правил используется оператор "+=", который означает не присваивание значения, а добавление значения. Аналогично оператор "– =" используется для удаления значения. Факторы уверенности в последнем случае объединяются по формуле

cfA*(100 – cfB)/100

Рассмотрим применение аппарата нечеткой логики на примере оценки надежности поставщика, где кроме фактора финансового состояния учитывается и фактор формы собственности. Допустим, что государственное предприятие не имеет задолженность с уверенностью 60 и предполагается, что его рентабельность удовлетворительна с уверенностью 80. Фрагмент правил имеет следующий вид:

Правило 1: Если Задолженность = "нет" и Рентабельность = "удовл." Знак??

То Финансовое_состояние = "удовл." cf 100

Правило 2: Если Финансовое_состояние = "удовл."

То Надежность += "есть" cf 90

Правило 3: Если Предприятие = "государств."

То Надежность+ = "есть" cf 50

Результат выполнения первого правила:

cf(посылки) = min(60,80) = 60,

cf(Фин_сост.="удовл.") = 60*100/100 = 60.

Результат выполнения второго правила:

cf(Надежность="есть") = 60*90/100 = 54

Результат выполнения третьего правила:

cf(Надежность="есть") = 54 + 50 – 54*50/100 = 67

Динамические модели. Моделирование рассуждений человека, как правило, не сводится только к прямой или обратной аргументации. Сложные проблемы решаются путем выдвижения во времени нескольких гипотез с анализом подтверждающих фактов и непротиворечивости следствий. Причем для многоцелевых проблемных областей происходит увязка гипотез по общим ограничениям. При этом возможны задержки в принятии решений, связанные со сбором подтверждающих фактов и/или доказательством подцелей, входящих в ограничения.

Следовательно, для подобных динамических проблем большое значение имеют рациональная организация памяти системы для запоминания и обновления получаемых промежуточных результатов, обмен данными между различными источниками знаний для достижения нескольких целей, изменение стратегий вывода от выдвижения гипотез (прямая аргументация) к их проверке (обратная аргументация). Для построения таких гибких механизмов вывода используют технологию типа "доски объявлений", в которой источники знаний обмениваются сообщениями.

В целях динамического реагирования на события некоторые продукционные модели используют специальные правила-демоны (приложение 2), которые формулируются следующим образом:

"Всякий раз, как происходит некоторое событие, выполнить некоторое действие". Например:

Всякий раз, как становится известным значение

переменной "Поставщик",

Выполнить набор правил "Финансовый анализ предприятия".

В программной среде GURU подобное правило будет записано следующим образом:

IF: KNOWN(“Поставщик”) = true

THEN: CONSULT FIN_AN

Для динамических экспертных систем характерна также обработка времени как самостоятельного атрибута аргументации логического вывода.

Рис. 2.6. Пример семантической сети

Общим недостатком всех формализмов представления знаний, основанных на правилах, является недостаточно глубокое отражение семантики проблемной области, что может сказываться на гибкости формулирования запросов пользователей к экспертным системам. Этот недостаток устраняется в объектно-ориентированных методах представления знаний.

Семантические сети. Объектно-ориентированные методы представления знаний берут начало от семантических сетей, в которых типизируются отношения между объектами. Элементарной единицей знаний в семантической сети служит триплет (см. объектную концептуальную модель), в котором имя предиката представляет собой помеченную дугу между двумя узлами графа, соответствующими двум связанным объектам(рис. 2.6).

Важнейшими типизированными отношениями объектов являются: "Род" – "Вид", "Целое" – "Часть", "Причина" – "Следствие", "Средство" – "Цель", "Аргумент" – "Функция", "Ситуация" – "Действие". Типизация отношений позволяет однозначно интерпретировать смысл отображаемых в базе знаний ситуаций и настраивать механизм вывода на особенности этих отношений. Так, отображение отношений "Род" – "Вид" дает возможность осуществлять наследование атрибутов классов объектов и, таким образом, автоматизировать процесс вывода заключений от общего к частному.

Фреймы. Развитием семантических сетей являются фреймовые методы представления знаний, в которых все атрибуты (поименованные отношения) объектов собираются в одну структуру данных, называемую фреймом. Причем в качестве значений слотов (атрибутов) могут выступать как обычные значения данных, так и действия, направленные на получение этих значений. Действия реализуются в виде присоединенных процедур или процедур-демонов, вызываемых по определенным условиям. В этом плане фреймовый метод представления знаний в большей степени операционно ориентирован по сравнению с семантической сетью.

Неопределенность описания знаний реализуется в результате неполного заполнения всех слотов. Фреймовая модель способна делать предположения о значениях данных на основе механизма наследования свойств в иерархии обобщения. В качестве способов наследования атрибутов применяются следующие: S – идентичные значения одноименных слотов; U – различные значения одноименных слотов; R – значение слота фрейма нижнего уровня должно находиться в пределах, заданных в одноименном слоте фрейма верхнего уровня; О – в случае неизвестности значения слота фрейма нижнего уровня принимается значение слота фрейма верхнего уровня.

Способность изменения значений слотов с течением времени позволяет решать динамические задачи. Во фреймовых моделях могут выполняться как прямая, так и обратная аргументация, когда в прямом направлении в зависимости от состояния слотов фреймов запускаются процедуры-демоны (неизвестно значение – "if-needed", известно значение – "if-added", удаляется значение – "if-removed), а обратная аргументация срабатывает путем запуска присоединенных процедур при обращении к неизвестным значениям атрибутов. Фреймовые модели позволяют более гибко комбинировать прямой и обратный выводы.

Объектно-ориентированная модель, аналогичная во многом фреймовой, предусматривает еще инкапсуляцию процедур в структуры данных и механизм наследования. Главное отличие заключаются в четком различии понятий "класс объектов" и "экземпляр объекта", а также в способе активации процедур к объектам. Для объектно-ориентированной модели характерны такие возможности, как скрытие данных и их доступность только через методы (присоединенные процедуры) класса, наследование как атрибутов, так и методов (в последнем случае обеспечивается необходимый уровень абстракции данных и полиморфизм использования процедур). Обращение к объектам, т. е. вызов методов класса, осуществляется либо из внешних программ, либо из других объектов путем посылки сообщений.