Задание 2. Рекурсивные функции

1. Записать алгоритм Евклида вычисления наибольшего общего делителя (НОД) как рекурсивную функцию. Алгоритм основан на том факте, что если a=qb+r, где 0<r<b, то HOD(a,b)=HOD(b,r). В процессе вычислений выводить на экран текущие выражение a=qb+r в численном виде, то есть 37=2*17+3, 17=5*3+2 и т.д. В конце вывести НОD.

2. Записать алгоритм, проверящий является ли заданное число простым как рекурсивную функцию. Вывести на экран все простые числа, не превосходящих n.

3. Записать алгоритм разложения произвольного числа на простые множители как рекурсивную функцию с выводом на экран сомножителей.

4. Записать алгоритм нахождения канторового разложения произвольного числа а – вектора 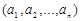в виде рекурсивной функции. Канторовым разложением положительного числа а называется запись вида: , .

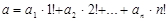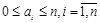5. Определить рекурсивную функцию, которая возвращает факториал целого неотрицательного числа. Написать программу, вычисляющую 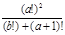по заданным a и b.

6. Определить рекурсивную функцию, вычисляющую число сочетаний 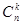, используя соотношение .

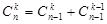7. Определить рекурсивную функцию, которая возвращает n-ое число Фибоначчи. Числа Фибоначчи вычисляются следующим образом: .

8. Определить рекурсивную функцию, которая вычисляет сумму цифр натурального числа.

9. Определить рекурсивную функцию, выводящую на экран цифры целого положительного числа.

10. Определить рекурсивную функцию, которая находит корень уравнения f(x)=0 на заданном интервале [a,b] c заданной точностью e. Корень ищется методом деления отрезка пополам по следующему алгоритму. Первоначально предполагается, что f(a)f(b)<0.

1) вычисляются f(а), f(b);

2) вычисляется c=(a+b)/2 и f(c);

3) если f(a)f(c)>0, то а=c, в противном случае b=c;

4) если b-a>e, то перейти к шагу 2, иначе любой из концов отрезка может быть использован в качестве корня уравнения.

11. Определить рекурсивную функцию, выводящее в экран двоичное представление заданного десятичного числа.

12. Определить рекурсивную функцию, возвращающую максимальное из n чисел.