Задание 3. Применение разветвляющихся алгоритмов при решении простейших задач

1. Даны числа 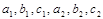. Определить, коллинеарны ли вектора с такими координатами.

2. Значение переменных a,b,c поменять местами так, чтобы оказалось .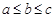

3. По номеру некоторого года определить номер его столетия (учесть, что, к примеру, началом 20-го столетия был 1901, а не 1900 год).

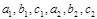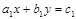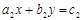4. Даны числа . Выяснить, являются ли прямые, описываемые уравнениями и параллельными, перпендикулярными, просто пересекаются либо совпадают.

5. По трем введенным вещественным числам выяснить, можно ли построить треугольник с такими длинами сторон, и, если можно, то какой: равносторонний, равнобедренный, прямоугольный или общего вида.

6. Даны числа 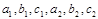. Определить, равны ли вектора с такими координатами.

7. Введите свой месяц и день рождения. Определите, является ли ваш день рождения очень счастливым, просто счастливым или обычным. День считается очень счастливым, если остатки от деления на 7 сумм цифр месяца и дня совпадают, просто счастливым, если хотя бы один из этих остаток равен 0, и обычным в противном случае.

8. Определить, имеют ли поля шахматной доски (n₁,m₁) и (n₂,m₂) одинаковый цвет. (n₁,m₁, n₂,m₂ – натуральные числа от 1 до 8).

9. Определить, угрожает ли слон, расположенный на поле (n₁,m₁) шахматной доски, фигуре, расположенной на поле (n₂,m₂). (n₁,m₁, n₂,m₂ – натуральные числа от 1 до 8).

10. Определить, угрожает ли ферзь, расположенный на поле (n₁,m₁) шахматной доски, фигуре, расположенной на поле (n₂,m₂). (n₁,m₁, n₂,m₂ – натуральные числа от 1 до 8).

11. Определить, угрожает ли конь, расположенный на поле (n₁,m₁) шахматной доски, фигуре, расположенной на поле (n₂,m₂). (n₁,m₁, n₂,m₂ – натуральные числа от 1 до 8).

12. Даны три вещественных числа a,b,c. Вычислить сколько вещественных корней имеет квадратное уравнение 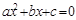или не имеет их вообще. Если вещественные корни существуют, вычислить их.