Геометричний і структурний підходи

Щоразу, коли стикаються з незнайомими завданнями, з'являється природне бажання представити їх у вигляді деякої легко зрозумілої моделі, яка дозволяла б осмислити завдання в таких термінах, які легко відтворюються нашою уявою. Завдяки тому, що ми існуємо в просторі й у часі, найбільш зрозумілою для нас є просторово-часова інтерпретація завдань.

Будь-яке зображення, що виникає в результаті спостереження якого-небудь об’єкту в процесі навчання або випробування, можна представити у вигляді вектора, а значить і у вигляді точки деякого простору ознак. Якщо стверджується, що при показі зображень можливо однозначно віднести їх до одного з двох (або декількох) образів, то тим самим стверджується, що в деякому просторі існує дві (або декілька) області, що не мають загальних точок, і що зображення – точки із цих областей. Кожній такій області можна приписати найменування, тобто дати назву, що відповідає образу.

Проінтерпретуємо тепер у термінах геометричної картини процес навчання розпізнаванню образів, обмежившись поки випадком розпізнавання тільки двох образів. Заздалегідь вважається відомим тільки те, що потрібно розділити дві області в деякому просторі, і що показуються точки тільки із цих областей. Самі ці області заздалегідь не визначені, тобто немає яких-небудь відомостей про розташування їхніх границь або правил визначення належності точки до тієї чи іншої області.

У ході навчання пред'являються точки, випадково обрані із цих областей, і повідомляється інформація про те, до якої області належать пропоновані точки. Ніякої додаткової інформації про ці області, тобто про розташування їхніх границь, у ході навчання не повідомляється. Мета навчання полягає або в побудові поверхні, що розділяла б не тільки показані в процесі навчання точки, але й усі інші точки, що належать цим областям, або в побудові поверхонь, що обмежують ці області так, щоб у кожній з них перебували тільки точки одного образу. Інакше кажучи, мета навчання полягає в побудові таких функцій від векторів-зображень, які були б, наприклад, позитивні на всіх точках одного і негативні на всіх точках іншого образу. У зв'язку з тим, що області не мають загальних точок, завжди існує ціла множина таких поділяючих функцій, а в результаті навчання повинна бути побудована одна з них.

Якщо зображення належать не двом, а більшому числу образів, то завдання полягає в побудові по показаних у ході навчання точках поверхні, що розділяє одну від одної всі області, які відповідають цим образам. Завдання це може бути вирішене, наприклад, шляхом побудови функції, що приймає над точками кожної з областей однакове значення, а над точками з різних областей значення цієї функції повинне бути різним.

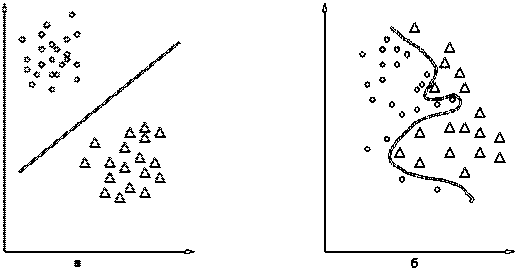
Рис. 2. Два образи

На перший погляд здається, що знання всього лише деякої кількості точок з області недостатньо, щоб відокремити всю область. Дійсно, можна вказати незліченну кількість різних областей, які містять ці точки, і як би не була побудована по них поверхня, що виділяє область, завжди можна вказати іншу область, що перетинає поверхню й разом з тим містить показані точки. Однак відомо, що завдання про наближення функції за інформацією про неї в обмеженій множині точок, істотно більш вузьке, ніж вся множина, на якій функція задана, є звичайним математичним завданням про апроксимацію функцій. Зрозуміло, рішення таких завдань вимагає введення певних обмежень на класі розглянутих функцій, а вибір цих обмежень залежить від характеру інформації, що може додати вчитель у процесі навчання. Однією з таких підказок є гіпотеза про компактність образів. Інтуїтивно ясно, що апроксимація поділяючої функції буде завданням тим більше легшим, чим більше компактні і чим більше рознесені в просторі області, що підлягають поділу. Так, наприклад, у випадку, показаному на рис. 2а, поділ свідомо більш простий, ніж у випадку, показаному на рис. 2б. Дійсно, у випадку, зображеному на рис. 2а, області можуть бути розділені площиною, і навіть при більших погрішностях у визначенні поділяючої функції вона все-таки буде продовжувати розділяти області. У випадку ж рис. 2б поділ здійснюється складною поверхнею і навіть незначні відхилення в її формі приводять до помилок поділу. Саме це інтуїтивне подання про порівняно легко роздільні області привело до гіпотези компактності.

Поряд з геометричною інтерпретацією проблеми навчання розпізнаванню образів існує й інший підхід, що названий структурним, або лінгвістичним. Пояснимо лінгвістичний підхід на прикладі розпізнавання зорових зображень. Спочатку виділяється набір вихідних понять – типових фрагментів, що зустрічаються на зображеннях, і характеристик взаємного розташування фрагментів – "ліворуч", "знизу", "усередині" і т.п. Ці вихідні поняття утворять словник, що дозволяє будувати різні логічні вирази, які іноді називають припущеннями. Завдання полягає в тому, щоб з великої кількості виразів, які могли б бути побудовані з використанням цих понять, відібрати найбільш істотні для даного конкретного випадку.

Далі, переглядаючи кінцеве й по можливості невелике число об'єктів з кожного образу, потрібно побудувати опис цих образів. Побудовані описи повинні бути настільки повними, щоб вирішити питання про те, до якого образу належить даний об'єкт. При реалізації лінгвістичного підходу виникають два завдання: завдання побудови вхідного словника, тобто набір типових фрагментів, і завдання побудови правил опису з елементів заданого словника.

У рамках лінгвістичної інтерпретації проводиться аналогія між структурою зображень і синтаксисом мови. Прагнення до цієї аналогії було викликане можливістю використати апарат математичної лінгвістики, тобто методи по своїй природі є синтаксичними. Використання апарату математичної лінгвістики для опису структури зображень можна застосовувати тільки після того, як зроблена сегментація зображень на складові частини, тобто вироблені слова для опису типових фрагментів і методи їхнього пошуку. Після попередньої роботи, що забезпечує виділення слів, виникають лінгвістичні завдання, що складаються із завдань автоматичного граматичного розбору описів для розпізнавання зображень. При цьому проявляється самостійна область досліджень, що вимагає не тільки знання основ математичної лінгвістики, але й оволодіння прийомами, які розроблені спеціально для лінгвістичної обробки зображень.