Нелинейные случайные функции
Для многих объектов типична некоторая постоянная относительная скорость изменения ОП
что соответствует нелинейному случайному процессу Х(t), аппроксимируемому случайной функцией вида
| (14.6) |
где Х0 = Х(t=0) = {x}0 - как и ранее, случайное начальное значение ОП; V' - случайная, нормально распределенная скорость изменения натурального логарифма ОП во времени, имеющая МО mv = M{V} и СКО Sv = 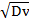 .
.
В моделях обоих классов (14.5) и (14.6) знаки "+" и "-" используются для аппроксимации соответственно возрастающих и убывающих во времени процессов. Случайная величина Х0 в моделях (5), (6) является постоянной во времени, как и случайная величина скорости V изменения ОП в модели (14.5). В модели (14.6) постоянной во времени является скорость изменения логарифма ОП, сам же ОП имеет переменную во времени скорость изменения.
В дальнейшем для простоты обозначения будем полагать, что
Для удобства дальнейшего рассмотрения моделей только в линейном варианте модель (14.6) путем логарифмирования преобразуем к линейной модели изменения логарифма ОП:
| (14.7) |
Обозначая натуральный логарифм ОП случайной функцией Y(t)
| (14.8) |
выражение (13.7) можно представить в виде
| (14.9) |
подобном модели (14.5).
Рассмотрим раздельно каждый тип линейных случайных моделей, аппроксимирующих случайный процесс изменения ОП Х(t) или его логарифма Y(t).
Дата добавления: 2015-10-09; просмотров: 820;
